sir Isaac Newton

Physicien, mathématicien et astronome anglais (Woolsthorpe, Lincolnshire, 1642-Londres 1727).

Figure majeure de l'histoire des sciences, Isaac Newton a fondé la mécanique classique avec sa théorie de l'attraction universelle (→ gravitation). Il a contribué aussi aux progrès de l'optique et de l'analyse mathématique, tout en consacrant beaucoup de temps à la théologie et à l'alchimie.

1. Jeunesse et formation de Newton

Né prématurément le jour de Noël, l'année même de la mort de Galilée, Newton est un enfant si chétif et malingre qu'on pense qu'il ne pourra pas vivre. Son père, propriétaire terrien, meurt avant sa naissance, et sa mère se remarie avec Barnabas Smith, recteur de North Witham. L'enfant, alors âgé de trois ans, est confié à sa grand-mère, qui lui fait faire ses premières études aux écoles primaires de Skilington et de Stoke, deux hameaux voisins de Woolsthorpe. À l'âge de douze ans, il est envoyé à l'école publique de Grantham et logé chez l'apothicaire de l'endroit. Il racontera lui-même qu'il était un élève fort peu attentif ; il préférait s'amuser à construire de petites machines, tels une espèce de clepsydre fort précise, un cadran solaire et un moulin mû par une souris qu'il appelait le « meunier » et qui, pour se nourrir, prélevait une partie de la farine qu'elle produisait. Il aimait aussi dessiner d'après nature ou selon son imagination, et les murs de sa petite chambre étaient couverts de dessins et de peintures.

Redevenue veuve en 1656, sa mère le rappelle à Woolsthorpe, pour l'employer à l'administration et aux travaux de la ferme. Mais ce genre d'occupation ne lui convient guère. Tandis qu'un vieux serviteur s'occupe des achats et des ventes dont on l'a chargé au marché de Grantham, Newton retourne chez son ancien hôte pour s'adonner à la lecture de vieux livres ou s'arrête même en chemin. La passion qu'il montre alors pour les sciences lui vaut, sur l'intervention d'un oncle, de poursuivre ses études à Grantham. Puis, à l'âge de dix-huit ans, il est envoyé au Trinity College de Cambridge, où il est vite distingué par son maître, le mathématicien Isaac Barrow (1630-1677). En 1665, il y obtient le degré de bachelier ès arts.

Cette même année, la peste sévit à Londres. L'université de Cambridge ferme ses portes, et Newton retourne à Woolsthorpe, où il reste jusqu'en 1667. C'est sans doute pendant cette période qu'il effectue ses principales découvertes. La tradition veut, notamment, qu'il ait eu l'idée de l'attraction universelle en voyant tomber une pomme : pourquoi la Lune, elle, ne tombe-t-elle pas ? Quelle est la force qui la maintient sur son orbite ? se serait-il alors demandé. Cette anecdote, rapportée à Voltaire par une nièce de Newton, n'a jamais été mentionnée par celui-ci et n'est probablement qu'invention. Néanmoins, Newton ne fait pas connaître les résultats qu'il obtient à cette époque, car il n'éprouve aucun besoin de publier. Comme l'a remarqué Fontenelle, on peut lui appliquer ce que Lucain a dit du Nil, dont les Anciens ne connaissaient point la source : « Qu'il n'a pas été permis aux hommes de voir le Nil faible et naissant. »

Après son retour à Cambridge, Newton acquiert les autres grades universitaires et obtient en 1669 la chaire de mathématiques, dont Barrow s'est dessaisi pour se consacrer à la théologie ; pendant vingt-six ans, il remplira avec zèle ses fonctions de professeur. En 1669, également, il rédige un compte rendu de ses découvertes mathématiques, le théorème du binôme généralisé et les fondements du calcul infinitésimal, pour le confier à Barrow ; ce compte rendu ne sera publié qu'en 1711.

2. L'optique de Newton

À ce moment, Newton s'occupe de perfectionner le télescope, et il en construit les lentilles de ses propres mains. Puis, en 1671, il pense à utiliser comme objectif un miroir sphérique, dénué d'aberrations chromatiques. Ce télescope est connu de la Royal Society, qui ouvre ses portes à son auteur en 1672.

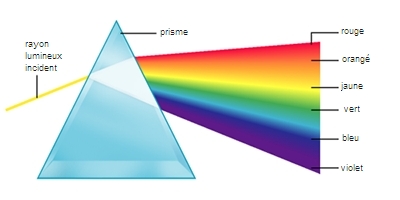
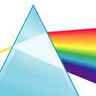
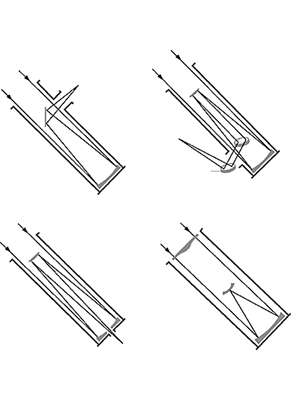
Encouragé par l'intérêt que lui manifeste cette glorieuse institution, Newton lui présente la première communication qui sera rendue publique ; il y expose ses expériences faites au moyen du prisme et prouvant que la lumière blanche est composée de rayons colorés dont la réfrangibilité est différente. Cette affirmation suscite de vives controverses, notamment avec Robert Hooke et avec Christiaan Huygens, et Newton, qui déteste les discussions et ne supporte guère la contradiction, « blâme sa propre imprudence, qui l'a poussé à abandonner un bien aussi solide et substantiel que sa tranquillité, pour courir après une ombre ».

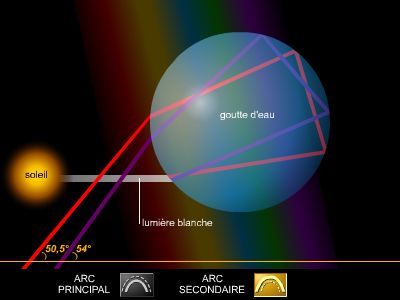
Cependant, en 1675, il publie un nouveau travail sur la lumière, où figure sa théorie corpusculaire, ou théorie de l'émission. Toutefois, pour expliquer les irisations des lames minces et l'expérience d'interférences dite « des anneaux de Newton », il attribue aux particules lumineuses certaines propriétés ondulatoires, faisant déjà une synthèse de ces deux aspects « complémentaires » de la lumière. En même temps, il donne une théorie de la couleur des corps et complète l'explication de l'arc-en-ciel fournie par Descartes. Tous ces travaux d'optique ainsi que ses observations sur la diffraction de la lumière, qu'avait découverte Grimaldi, figureront dans son grand ouvrage Opticks, dont il ajourne la publication jusqu'en 1704, après la mort de Hooke.

3. L'attraction universelle et les « Principes »

Ayant achevé l'essentiel de son œuvre en optique, Newton semble se désintéresser de la science. Mais l'astronome Edmund Halley (1656-1742), à la suite de discussions avec Hooke et Christopher Wren (1632-1723), va le consulter à Cambridge au sujet des fameuses lois de Kepler et des orbites elliptiques des planètes. Les réponses de Newton sont à ce point convaincantes que Halley le presse, en 1685, de publier ses découvertes sur la gravitation et se charge de payer les frais d'impression. Et c'est en 1687 que paraît l'œuvre immortelle de Newton : Philosophiae naturalis principia mathematica (→ Principes mathématiques de la philosophie naturelle).

• 
• 

Dans la préface de ces trois volumes, Newton expose qu'il veut appliquer les mathématiques à l'étude des phénomènes naturels, parmi lesquels le mouvement occupe le premier rang. La force, dont l'origine et la nature nous restent inconnues, y est définie uniquement par ses manifestations. On trouve dans cet ouvrage le principe d'inertie, la proportionnalité des forces et des accélérations, l'égalité de l'action et de la réaction. Newton y développe sa théorie de l'attraction universelle (→ gravitation) et la loi de l'inverse carré, d'où se déduisent les trois lois de Kepler sur le mouvement des planètes.

Cet ouvrage expose aussi les lois du choc, étudie le mouvement des fluides (→ mécanique des fluides), calcule la précession des équinoxes et l'aplatissement terrestre (→ Terre), donne la théorie des marées, établit l'orbite des comètes, explique les perturbations planétaires, etc. On est en droit d'affirmer que ces Principes ont posé les fondements et fixé les méthodes de la science moderne. Comme l'a écrit Laplace : « L'importance et la généralité des découvertes, un grand nombre de vues originales et profondes qui ont été le germe des plus brillantes théories de ce siècle, tout cela, présenté avec beaucoup d'élégance, assure à l'ouvrage la prééminence sur les autres productions de l'esprit humain. »

4. Newton mathématicien

La tradition historique veut qu'Isaac Newton doive l'essentiel de sa formation mathématique à Isaac Barrow. La publication de ses manuscrits mathématiques de jeunesse montre qu'il n'en est rien. Dans le domaine des mathématiques supérieures, Newton est un parfait autodidacte, qui s'est formé par la lecture solitaire des principaux ouvrages contemporains. Sa connaissance des grands mathématiciens de l'Antiquité est très superficielle. Il ne connaîtra guère Archimède et Apollonios de Perga qu'après avoir approfondi les travaux des mathématiciens modernes. Il lira alors simplement les éditions modernisées d'Archimède et d'Apollonios dues à Barrow (1675).

Ses véritables maîtres sont François Viète (1540-1603), lu dans l'édition procurée en 1646 par Frans Van Schooten (1615-1660), l'algébriste anglais William Oughtred (vers 1574-1660), John Wallis (1616-1703), professeur à Oxford, et surtout Descartes, dont il a étudié minutieusement la Géométrie dans l'édition latine en deux volumes donnée en 1659-1660 par Van Schooten et ses disciples. De tous ses contemporains, Newton est celui qui assimile le mieux les méthodes analytiques de Descartes. Il éclaire les points laissés obscurs par son devancier et dote la géométrie analytique de son efficacité maximale. Dès 1667-1668, il s'attaque à la classification des cubiques, dont il donne des tracés corrects, avec asymptotes, inflexions, points doubles, points de rebroussement.

À partir des techniques cartésiennes du tracé des tangentes, il développe un algorithme de calcul différentiel applicable aux courbes algébriques et étudie la notion de courbure indépendamment de Christiaan Huygens. D'autre part, dès 1666, il aborde ses études sur les fluentes (nos fonctions dérivables) et leurs fluxions (leurs dérivées). Son ouvrage De analysis per aequationes infinitas, écrit en 1669, commence la systématisation de ses méthodes infinitésimales, et l'on peut dire que, vers 1670, Newton a fondé l'analyse moderne. Le « binôme de Newton », ou développement de (1 + x)ⁿ pour toute valeur rationnelle de n, a été découvert dès 1665. À partir de 1680, Newton se cherchera un style plus géométrique, celui qu'il adoptera dans ses Principes de 1687.

5. Autres recherches

Mais les mathématiques et la physique ne sont pas ses uniques préoccupations, et il consacre probablement une part égale de son temps à d'autres recherches d'intérêt relativement médiocre. Ses convictions religieuses et son tempérament mystique le poussent à effectuer des travaux de théologie, avec une adhésion cachée à l'arianisme (doctrine hérétique qui nie la divinité du Christ). Des ouvrages comme Chronology of Ancient Kingdoms Amended, 1728 ; Observations upon the Prophecies of Daniel, and the Apocalypse of St. John, 1733) lui coûtent sans doute autant d'efforts que les Principes, sans ajouter à sa gloire. Il porte aussi un grand intérêt à l'alchimie, comme en témoignent des manuscrits retrouvés au début du xx^e siècle, et il semble qu'il ait été à la recherche d'une sorte d'attraction universelle valable non plus à l'échelle cosmique mais à celle des constituants ultimes de la matière.

6. Newton dans sa vie publique

Après la parution des Principes, Newton semble de nouveau abandonner toute recherche scientifique. C'est l'époque de la fuite de Jacques II. En 1689, Newton va siéger à la Chambre des communes pour y représenter l'université de Cambridge. On rapporte qu'il y reste étranger aux débats et n'y prend qu'une fois la parole, pour inviter un huissier à fermer une fenêtre. Le Parlement est dissout, et nous savons par Huygens que Newton tombe alors, en 1692, dans une sorte de prostration – Biot parle même de folie –, causée peut-être par l'excès de son ancien travail, par la mort de sa mère ou par l'incendie accidentel du laboratoire où il poursuit ses recherches d'alchimie.

Cependant, un de ses anciens élèves, Charles Montagu, devenu lord Halifax, occupe en 1694 le poste de chancelier de l'échiquier, et son premier acte est de nommer son illustre maître inspecteur, puis, en 1699, directeur de la Monnaie. Newton abandonne alors sa chaire de Cambridge pour s'acquitter avec soin de cette nouvelle charge, au demeurant assez lucrative. Sa notoriété est devenue très grande : Newton est compris parmi les huit premiers associés étrangers de l'Académie des sciences de Paris (1699) ; en 1703, il est élu président de la Royal Society et le sera de nouveau chaque année jusqu'à la fin de sa vie ; enfin, en 1705, il reçoit de la reine Anne le titre de baronnet.

Newton, qui ne s'est jamais marié, meurt après de vives souffrances liées à une inflammation pulmonaire et à la goutte à quatre-vingt-cinq ans, et il est inhumé en grande pompe à l'abbaye de Westminster, aux côtés des rois d'Angleterre.

7. Citations