Archimède


Savant de l'Antiquité (Syracuse 287 avant J.-C.-Syracuse 212 avant J.-C.).
Figure emblématique de la science grecque antique, Archimède s'est illustré à la fois par d'importantes découvertes en mathématiques et en physique et par une série d'inventions très ingénieuses.
1. Archimède, disciple de l'école d'Alexandrie
Fils de l'astronome Phidias – qui avait calculé le rapport existant entre les dimensions du Soleil et de la Lune – et peut-être apparenté à Hiéron, tyran de Syracuse, Archimède est soumis dans sa jeunesse à l'influence, alors considérable, de l'école d'Alexandrie. Il est probable qu'il va lui-même séjourner dans cette ville d'Égypte et y suivre l'enseignement du mathématicien grec Euclide et de Conon de Samos. Peut-être se rend-il aussi en Espagne, mais il revient dans sa ville natale et ne va plus la quitter.
Il y vit dans l'entourage des souverains qui le protègent et, libre de tout souci matériel, il peut se consacrer entièrement à la recherche scientifique, exerçant ses talents dans des domaines aussi divers que la géométrie, la physique et la mécanique. On ne dispose pas de témoignages directs sur sa vie, mais seulement de récits ultérieurs, dont ceux de l'historien romain Tite-Live et du Grec Plutarque.
2. Archimède mathématicien
Archimède est d'abord un géomètre. Il est le premier, dans son ouvrage Sur la mesure du cercle, à donner une méthode permettant d'obtenir une approximation aussi grande que l'on désire du chiffre π, grâce à la mesure des polygones réguliers circonscrits à un cercle ou inscrits dans celui-ci ; utilisant les polygones à 96 côtés, il fournit une valeur de π comprise entre 22/7 et 223/71.
Dans son traité Sur la sphère et le cylindre, il prouve que le volume d'une sphère vaut les deux tiers du volume du cylindre circonscrit. Il accorde même à cette découverte une importance particulière, puisqu'il demande qu'une représentation d'un cylindre circonscrit à une sphère soit gravée sur sa tombe.
Dans l'Arénaire, Archimède cherche à calculer le nombre de grains de sable contenus dans l'Univers, tel qu'il se l'imagine ; pour représenter un nombre aussi grand (de l'ordre de 1063), il perfectionne le système numéral grec, qui utilise des lettres, en faisant appel aux exposants. Il trouve les formules d'addition et de soustraction des arcs, calcule l'aire d'un segment de parabole, d'un secteur de la spirale qui porte son nom, du cylindre, de la sphère, etc. Dans son traité Sur les sphéroïdes et sur les conoïdes, il étudie les ellipsoïdes, les paraboloïdes et les hyperboloïdes de révolution. Ses recherches sur les tangentes et les quadratures l'amènent à envisager le calcul différentiel et intégral, développé deux mille ans plus tard par l'Anglais Newton et l'Allemand Leibniz.
Pour en savoir plus, voir l'article analyse [mathématiques].
3. Archimède physicien
Mécanique, optique, hydrostatique
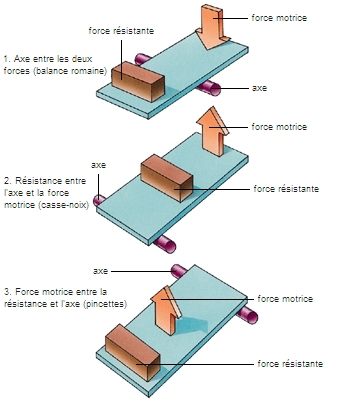
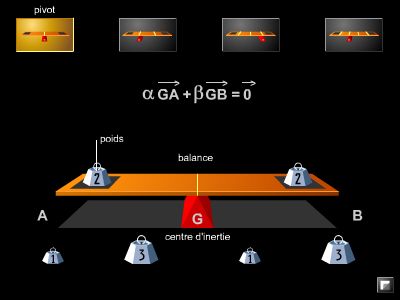
En physique, Archimède est le fondateur de la statique du solide, avec sa règle de la composition des forces et sa théorie du centre de gravité. Dans son premier livre, De l'équilibre des plans, il donne une théorie du levier : par abstraction, il réduit cet instrument à un segment de droite, en trois points duquel sont appliquées des forces qui s'équilibrent ; il montre, par ailleurs, que la balance n'en constitue qu'un cas particulier.
Archimède pose aussi les bases de l'hydrostatique, dans son traité Sur les corps flottants. Il indique notamment que la surface d'une eau tranquille est une portion de sphère dont le centre coïncide avec celui de la Terre.
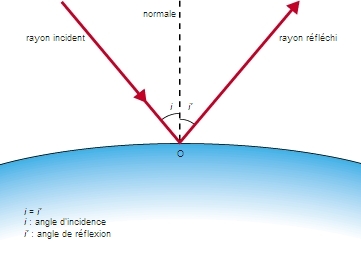
Outre ses œuvres déjà citées, on peut signaler la Catoptrique, étude de la réflexion de la lumière, les Polyèdres, la Méthode, lettre écrite à Ératosthène, ainsi que des ouvrages aujourd'hui perdus, la Sphéropée, qui traitait de mécanique appliquée, et les Principes, dédiés à un certain Zeuxippe.
En dépit des conseils du tyran de Syracuse Hiéron, qui l'engageait à orienter son activité vers les applications, Archimède, comme les autres savants grecs de son temps, s'intéressa surtout à la recherche fondamentale. Mais, à l'inverse de ses confrères, pour qui la valeur d'une théorie se mesurait selon des critères d'esthétique, il fut le premier à faire un constant appel au contrôle de l'expérience.
Pour en savoir plus, voir l'article science.
« Eurêka ! » : le principe d'Archimède

L'architecte romain Vitruve rapporte les curieuses circonstances dans lesquelles Archimède aurait découvert le fameux principe qui porte son nom (→ principe d'Archimède). Le roi Hiéron II avait commandé à un artisan une couronne d'or et lui avait fourni le métal précieux nécessaire. Bien que l'objet achevé présentât le même poids que l'or, Hiéron soupçonnait l'homme d'avoir substitué de l'argent à une certaine quantité de métal jaune. Il fit part de son inquiétude à Archimède, lui demandant s'il pouvait découvrir la fraude, tout en conservant la couronne intacte.
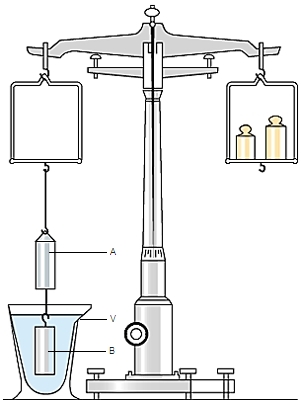
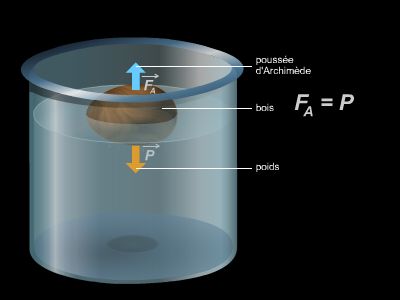
Le savant, méditant sur ce problème, fut frappé, en prenant son bain, par la diminution de poids que subissaient ses membres plongés dans l'eau. Il comprit alors que cette perte de poids équivalait au poids de l'eau déplacée. Et, dans l'enthousiasme de cette découverte, il se serait élancé nu dans la rue, en s'écriant : « Eurêka, eurêka ! » (« J'ai trouvé, j'ai trouvé ! »). En plongeant simultanément dans l'eau la couronne et un lingot d'or de même masse, maintenus à l'équilibre grâce à une balance romaine, Archimède put mesurer la différence de poids apparent entre les deux objets et prouver ainsi que l'orfèvre avait commis une supercherie.
4. Archimède ingénieur
La vis d'Archimède
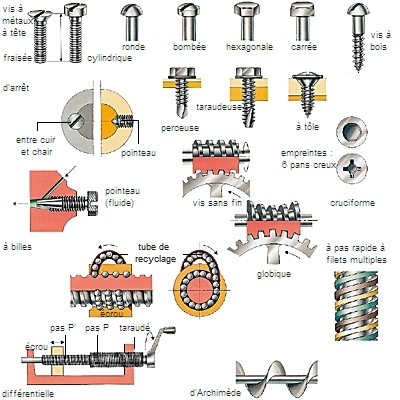
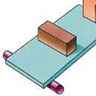
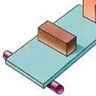
Éminent savant, à la fois théoricien et expérimentateur, Archimède est aussi un remarquable ingénieur. L'une de ses plus célèbres inventions est la vis sans fin, appelée aussi aujourd'hui vis d'Archimède, une hélice tournant autour de son axe et qui permet de déplacer des matériaux très divers, comme de l'eau ou de la pâte à papier.
L'historien grec Diodore de Sicile raconte qu'il conçut ce dispositif pour diriger les eaux du Nil sur les terrains que les inondations ne permettaient pas d'atteindre ; il semble qu'il l'utilisa également pour assurer la propulsion d'un vaisseau commandé par Hiéron.
Archimède a aussi introduit le boulon, formé d'une vis et d'un écrou, et la roue dentée.
La défense de Syracuse
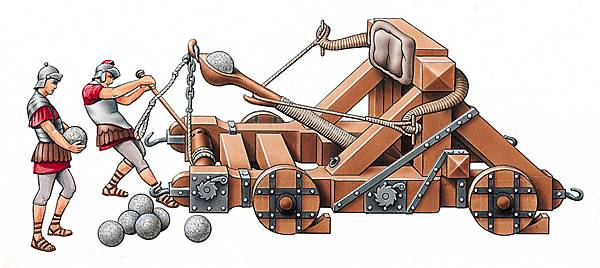
En 215 av. J.-C., Archimède organise la défense de Syracuse, attaquée par l'armée romaine. Pendant trois ans, il tient en échec les troupes du consul romain Marcellus. Il invente des catapultes capables de projeter d'énormes blocs rocheux à de grandes distances. Il réalise aussi une machine fonctionnant au moyen de leviers et de poulies et constituée de gros crochets en fer qui, lorsqu'un vaisseau ennemi s'avance jusqu'aux fortifications de la ville, s'en saisissent et le secouent violemment jusqu'à le briser. On raconte enfin – mais cela paraît plus douteux – qu'à l'aide de miroirs plans judicieusement disposés (miroirs ardents), il serait parvenu à concentrer sur les vaisseaux ennemis la lumière solaire et à les incendier.
Cependant, les Romains ayant pénétré par surprise dans la ville, Marcellus ordonne qu'on épargne Archimède, dont il admire le génie et qu'il espère gagner à la cause de Rome. Mais le savant, absorbé par la résolution d'un problème, est tué par un soldat qui, ne l'ayant pas reconnu, s'irrite de son refus de le suivre. Marcellus lui organisera de grandes funérailles et lui fera dresser un tombeau décoré de sculptures évoquant ses travaux. En 75 av. J.-C., Cicéron, questeur en Sicile, retrouvera cette tombe, envahie par les broussailles, et la fera restaurer.
Citations
Donnez-moi un point d'appui et je soulèverai la Terre !
Archimède, cité par Pappus (ive siècle)
De tous les grands hommes de l'Antiquité, Archimède est celui qui mérite le plus d'être placé à côté d'Homère.
Jean d'Alembert
Ceux qui sont en état de comprendre Archimède admirent moins les découvertes des plus grands hommes modernes.
Gottfried Wilhelm Leibniz