mathématiques
Science qui étudie par le moyen du raisonnement déductif les propriétés d'êtres abstraits (nombres, figures géométriques, fonctions, espaces, etc.) ainsi que les relations qui s'établissent entre eux.
Introduction
L'évolution des mathématiques, sur plus de vingt-cinq siècles, a été considérable. Non seulement elles ont donné lieu à une impressionnante quantité d'inventions et de découvertes, mais la constitution même de cette science a été modifiée. Les mots qui servent à désigner ses branches (algèbre, géométrie, etc.) ont en grande partie changé de sens. Un survol de leur évolution aide à comprendre cette diversité de sens. Une connaissance plus fine de leur histoire permettrait de saisir aussi combien des mots comme « fonction » ou « mesure » ont pu changer de signification.
Historique
Tout au long de leur histoire, les mathématiques offrent un double aspect. Elles sont d'abord une science, la plus théorique de toutes sans doute : elles traquent la vérité à propos d'objets fort peu naturels. D'un autre côté, le souci de mettre au point des procédés pratiques efficaces, calculatoires notamment, pour répondre à des besoins de nature très diverse, n'a jamais cessé d'animer les recherches. Tantôt les deux genres de préoccupations s'accordent étroitement, tantôt leurs liens se relâchent.
L'Antiquité
La géométrie et l'arithmétique ont des origines pratiques indéniables. On les rencontre dans presque toutes les civilisations quelque peu évoluées (en Inde, en Chine, en Égypte, etc.). Des préoccupations s'approchant du mysticisme, comme en témoigne le cas de Pythagore et de ses disciples (vie s. avant J.-C.), ont pu également avoir un rôle moteur.
La particularité de la Grèce est de leur avoir donné une forme déductive, avec définitions, principes et théorèmes. Euclide (iiie s. avant J.-C.) rassembla tout le savoir théorique qui avait été ainsi élaboré. Les treize livres de ses Éléments allaient constituer la référence majeure jusqu'au xixe s., notamment pour la géométrie, dans le plan et dans l'espace.
Dans les Éléments, l'arithmétique est la science qui prend pour objet les propriétés des nombres dans toute leur généralité. Il s'agit alors exclusivement de nombres qui expriment la pluralité : les entiers, à partir de 2. La simple pratique des calculs, sous le nom de logistique, était abandonnée aux hommes de l'art.
Le Moyen Âge et la Renaissance
Les successeurs des Grecs furent d'abord les savants du monde arabe puis, grâce à ces derniers, l'Occident latin. Tout en recueillant l'héritage d'Euclide et des autres grands géomètres, tous consacrèrent beaucoup au développement de méthodes pratiques. La plus importante de toutes fut la numération décimale de position, importée des Indes, aux algorithmes si efficaces. À la longue, le calcul écrit supplanta les autres techniques telles que l'usage des jetons.
Égyptiens, Mésopotamiens et Grecs savaient déjà résoudre ces petits problèmes qui, pour nous, débouchent sur la résolution d'une équation. Des méthodes approximatives leur donnaient quelques succès pour les degrés un et deux. Dans la géométrie grecque, on trouvait des problèmes équivalents, débouchant sur des constructions à la règle et au compas. Celui de la quadrature du cercle (construire un carré égal en aire à un cercle donné) fut un de leurs plus célèbres échecs.
Les Arabes réussirent à traiter de manière systématique les équations du second degré. Leur algèbre, comme on dit depuis, consistait en une méthode de manipulation des nombres, confirmée en parallèle par une preuve géométrique de sa validité. Il ne s'agissait pas encore de calculs littéraux : on exposait avec des mots, sur un exemple. Mais les calculs numériques, néanmoins, étaient devenus plus hardis : on opérait avec des fractions, parfois même avec des racines. Les Italiens, au xvie s., s'attaquèrent avec succès aux équations du troisième et du quatrième degré, inventant les nombres complexes pour pouvoir passer outre aux difficultés. Cette longue période a donc surtout vu se réaliser un superbe progrès désordonné, mais considérable, de la « logistique ».
La période classique
L'époque de la fin de la Renaissance vit apparaître d'autres nouveautés, comme les logarithmes. Deux d'entre elles allaient conduire à la naissance de l'analyse, destinée à supplanter arithmétique et géométrie : l'une fut l'usage des lettres en algèbre ; l'autre fut l'habitude qui se prit alors de ne pas hésiter à mêler l'infini aux calculs. On se mit notamment à user des séries, c'est-à-dire de sommes comportant une infinité de termes et prenant néanmoins une certaine valeur. Ainsi de la somme de fractions
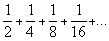qui, lorsque l'on ajoute des termes toujours diminués de moitié, donne 1.
René Descartes (1596-1650) combina la nouvelle algèbre avec la géométrie, créant ainsi la géométrie analytique. Cette dernière, avec ses équations de courbes, conduisit tout naturellement à la notion de fonction. C'est pour en déployer les potentialités que Isaac Newton (1642-1727) et Gottfried Wilhelm Leibniz (1646-1716) mirent au point le calcul infinitésimal. L'analyse, regroupement de toutes ces nouveautés, offrit le vaste champ de ses méthodes et de ses problèmes : limites, dérivation, intégration, équations différentielles, développements en série, etc. La géométrie et la mécanique en bénéficièrent pleinement.
La période moderne
L'expansion quantitative n'a fait que s'accélérer depuis. Un souci de rigueur accrue, qui se fit jour au xixe s., allait conduire à de nouvelles créations en même temps qu'à un bouleversement des mathématiques.
L'exigence de rigueur s'exerça d'abord sur les bases de l'analyse, laquelle n'avait été, quant à sa démarche, qu'une nouvelle logistique. Toutes les catégories de nombres reçurent enfin une définition solide ; en particulier les réels, grâce à Richard Dedekind (1831-1916) et à Georg Cantor (1845-1918). Non seulement l'analyse, mais même la géométrie (par un renversement de la géométrie analytique) pouvaient ainsi recevoir des bases bien organisées.
C'est vers la même époque que la découverte des géométries non euclidiennes commença d'ébranler la confiance en la vérité des mathématiques. Il devenait patent que cette science ne pouvait plus recevoir pour fondements que des axiomes, principes que l'on pose librement comme prémisses aux développements déductifs. L'Italien Giuseppe Peano (1858-1932) le réalisa pour l'arithmétique et l'Allemand David Hilbert (1862-1943) pour la géométrie.
Les ensembles, promus par Cantor en cette même fin de siècle, se révélèrent de bien meilleurs objets élémentaires que les entiers et les figures. L'équipe Bourbaki en vint à procéder à une reconstruction de la totalité des mathématiques à partir des ensembles. Ainsi peut-on y jouer depuis sur tous les degrés possibles de généralité, ce qui confère unité, souplesse et puissance.
Cette reconstruction a bénéficié, en plus de l'invention décisive des ensembles infinis, de trois développements. L'algèbre, après avoir porté sur les calculs littéraux, tendait à devenir la science des opérations elles-mêmes. En second lieu, l'étude des équations algébriques et celle des invariances géométriques avaient conduit à remarquer l'importance des groupes de transformations. Une troisième nouveauté, appelée à jouer un rôle d'importance, fut la topologie ; elle s'intéressait au départ à des problèmes de positions qui la conduisirent à relativiser l'importance des formes géométriques dans certaines questions. Le point commun à ces trois avancées est à repérer dans une certaine évanescence de l'objet initialement étudié : le nombre en algèbre, au profit de l'opération ; les équations d'un côté et les figures de l'autre, dans le cas des groupes, au profit des transformations ; la forme de la figure, enfin, qui perd en quelque sorte sa rigidité. Ainsi s'opérait une certaine décomposition de l'objet traditionnel des mathématiques, qui allait permettre et appeler une recomposition autour de nouveaux objets : les ensembles et les relations.
Les mathématiciens se sont livrés, en même temps qu'à cette vaste réorganisation, à un travail de fondation. Le besoin s'en faisait sentir depuis que les géométries non euclidiennes avaient mis à mal l'idée de vérité mathématique. Estimant que tout pouvait se réduire au nombre, les logicistes, avec l'Allemand Gottlob Frege (1848-1925) et le Britannique Bertrand Russell (1872-1970), entreprirent de faire sortir celui-ci de la logique. Il est vrai que cette dernière était enfin devenue une science, très mathématique d'allure, et qu'elle apparaissait comme science de la pensée pure. Les intuitionnistes, ou constructivistes, avec le Néerlandais Luitzen Brouwer (1881-1966), refusèrent cette réduction et pratiquèrent une logique un peu modifiée. Mais les mathématiciens ont plutôt suivi Hilbert dans sa tentative formaliste. Son but était de prouver, par le développement d'une métamathématique, que les mathématiques elles-mêmes ne risquaient pas de contenir une contradiction qui, en se révélant un jour, les aurait ruinées. Si cet aspect du projet n'a pas eu tout le succès escompté, la conception d'ensemble des mathématiques qui y est cultivée a largement prévalu.
Les mathématiques aujourd'hui
Les mathématiques, telles qu'un traité complet peut les exposer aujourd'hui, commencent par les ensembles, éventuellement accompagnés de la logique. Elles continuent par l'étude des structures générales, topologiques, algébriques ou d'ordre. Puis viennent les nombres et tout ce qui peut se produire par l'entrecroisement de ces premières branches.
La logique
Plus ou moins tenue pour une branche des mathématiques, en charge de la rigueur de ces dernières, la logique étudie la structure des propositions et celle des théories déductives. La logique dont les mathématiques ont besoin est bivalente : une proposition est soit vraie soit fausse, quelque sens que l'on donne à ces mots. Elle n'est pas modale : ni la temporalité ni le souhait n'y ont leur place.
La structure déductive d'une théorie s'examine à l'aune de règles telles que celle du modus ponens : des théorèmes A et (A ⇒ B) on peut déduire le théorème B. Il s'agit là du point de vue que l'on appelle syntaxique : le travail se réalise au niveau le plus formel possible. Le point de vue sémantique s'intéresse, sinon au sens à proprement parler, du moins à la possibilité pour une proposition d'être vraie dans une interprétation donnée du système symbolique.
Les ensembles
La théorie des ensembles la mieux acceptée est celle de Zermelo-Fraenkel (ZF). On adjoint généralement à ses axiomes celui du choix, nécessaire pour pouvoir démontrer, en tous domaines, nombre de théorèmes auxquels on tient. On forme ainsi la théorie ZFC.
Les axiomes définissent la manière licite de produire des ensembles, notamment par les opérations telles que l'intersection. La suite de la théorie des ensembles porte surtout sur les cardinaux, c'est-à-dire sur les nombres d'éléments des ensembles infinis, ainsi que sur les ordinaux, expressions des manières de classer ces éléments.
L'algèbre
L'algèbre générale n'est que le prolongement de la théorie des ensembles. Elle étudie les opérations qui peuvent se faire sur les ensembles eux-mêmes ainsi que les relations que l'on peut établir entre éléments de l'un et éléments d'un autre, ou bien entre éléments d'un même ensemble. Dans le premier cas se rangent surtout les fonctions, avec des catégories importantes, comme celle des bijections. Dans le second cas, les relations d'équivalence se distinguent par la possibilité qu'elles donnent d'effectuer des partitions, c'est-à-dire des découpages. Une fois cet arsenal disponible, on peut aborder l'étude des structures algébriques, c'est-à-dire des opérations et de leurs propriétés, toujours en toute généralité : structures de groupes, d'anneaux, de corps, d'espaces vectoriels. Avec ces derniers, on entre dans l'algèbre linéaire, très influencée dans ses idées et dans son vocabulaire par la géométrie des vecteurs. Par addition de propriétés supplémentaires, on enrichit les structures, au prix bien entendu d'une perte de généralité : plus on suppose de propriétés à des opérations, moins on rencontrera de situations pouvant entrer dans ce moule qu'est une structure.
La question des équations algébriques, autrement dit la bonne vieille algèbre, trouve sa place à ce niveau. Il n'est pas nécessaire de construire les nombres réels pour commencer d'étudier la factorisation des polynômes et la résolution des équations. Ces notions reçoivent une définition générale dans le cadre des structures d'anneau et de corps. Les théorèmes généraux ainsi établis s'appliqueront, en particulier, au cas des polynômes réels et à celui des polynômes complexes.
La topologie
La visée de la topologie générale est de fournir à l'analyse des bases larges. Elle traite, de la façon la plus abstraite possible, des questions de voisinage, de proximité, de limite, de continuité. Elle leur donne un sens dans les espaces topologiques, c'est-à-dire dans tout ensemble dans lequel on trouve des sous-ensembles satisfaisant à certaines conditions. L'usage des ensembles permet d'éviter complètement toute notion de distance, tout en ménageant la possibilité de prendre cette dernière en compte. Comme pour les structures algébriques, on peut enrichir à loisir les structures topologiques.
Les résultats s'appliquent, sans surprise, à des espaces tels que l'ensemble des réels. Mais les retombées vont bien au-delà. Les espaces topologiques sont tout aussi bien des ensembles de fonctions numériques : leurs « points » sont des fonctions.
Des branches plus spécialisées de la topologie la conduisent à se lier à d'autres branches, notamment à l'algèbre.
Les nombres
À partir des ensembles on sait reconstruire les entiers et, à partir de ces derniers, les rationnels, les réels, les complexes et d'autres encore.
L'arithmétique n'est plus, dans l'usage le plus courant, que l'étude des entiers. Lorsque cette science commence à faire appel à d'autres branches, dont l'analyse, pour trouver des solutions à ses problèmes, on l'appelle plutôt théorie des nombres. L'étude des rationnels est parfois considérée comme faisant partie de l'arithmétique, ce qui, jusqu'à un certain point, n'entraîne aucun inconvénient. Cette partie du langage des mathématiques n'a rien d'officiel. Elle ne donne pas lieu à des définitions en bonne et due forme, parce que le découpage des mathématiques que ces mots opèrent n'est guère important : on ne leur demande que de fournir un vague repérage.
Analyse, probabilités, géométrie…
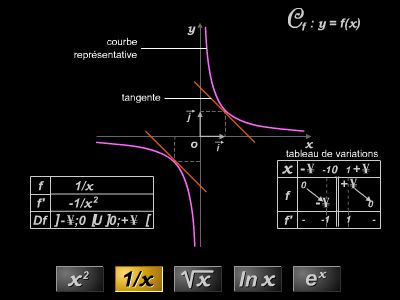
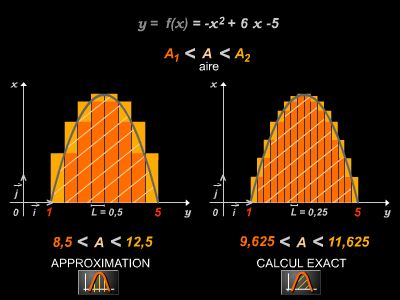
L'étude classique des fonctions, à variables réelles ou complexes, bénéficie de la puissance de la topologie. L'intégrale, par exemple, a pu être définie dans le cadre très général des espaces topologiques. De nombreux théorèmes relatifs aux intégrales peuvent ainsi se voir démontrer en une seule fois.
Nées au xviie s. en tant que calcul des chances, les probabilités ont reçu leurs bases axiomatiques précises, permettant une déduction impeccable de leurs théorèmes. On n'a besoin pour cela que des ensembles et des nombres réels, sans aucune allusion aux boules et aux urnes. Cela n'empêche pas d'employer un vocabulaire marqué par les origines réelles : on parle toujours d'événements ; mais ce ne sont plus que des sous-ensembles d'un ensemble qui peut être des plus quelconques. Le maintien de ce vocabulaire n'est d'ailleurs pas seulement la conséquence des habitudes prises : il aide à faire le lien entre la théorie et l'application pratique.
La structure d'espace affine, définie à partir de la notion d'espace vectoriel, est une reconstruction de la droite, du plan et de l'espace de la géométrie traditionnel. Mais son caractère très général va jusqu'à les appauvrir. La notion de distance, par exemple, n'est introduite que dans une étape ultérieure, celle des espaces affines euclidiens. Il faut ensuite que l'analyse vienne prêter main-forte pour que toute la richesse des courbes et des surfaces réapparaisse. La géométrie, qui avait été la science reine depuis Euclide, est de toutes les anciennes branches la plus écartelée.
L'activité mathématique
L'apprentissage des rudiments
L'acquisition du savoir d'un bachelier – qu'un mathématicien considère comme tout juste rudimentaire – s'étale sur plusieurs années dans la vie d'un jeune humain. La géométrie étudiée représente une petite fraction des Éléments, repensée en terme de transformations et rendue plus calculatoire que démonstrative par l'emploi des vecteurs. Ces deux améliorations nous viennent du xixe s. L'algèbre se limite au second degré ; c'est donc celle des Arabes mais pratiquée avec le calcul littéral. La géométrie analytique est à peu près celle que Descartes connaissait. L'analyse est celle de Newton et de Leibniz, moins les séries. Les probabilités, enfin, sont celles des débuts, avec Pascal et Fermat. Ce n'est qu'en passant dans l'enseignement supérieur que l'on découvre véritablement les ensembles ainsi que l'algèbre moderne.
Les mathématiques, les autres sciences et les techniques
Le développement de la recherche mathématique poursuit sa croissance. On estime à cent mille le nombre des théorèmes produits chaque année dans le monde. Corrélativement, la spécialisation va en s'accentuant, comme pour toute l'activité scientifique. La recherche se scinde en recherche pure et recherche appliquée, cette dernière concernant les autres sciences ainsi que les techniques.
Depuis le xviie s., la physique est une science mathématisée : ses concepts de base sont des grandeurs (par exemple, la vitesse) ou le sont devenus (les couleurs). La mécanique céleste a été la première science de la nature à profiter pleinement de la richesse de moyens offerte par l'analyse. Au xxe s., la physique, et la cosmologie à sa suite, ont pu envisager un univers à quatre dimensions, non euclidien. Il n'est pas jusqu'aux sciences humaines, telle l'économie ou la sociologie, qui n'aient tenté de conquérir leur brevet de haute scientificité par le biais de la mathématisation. Certaines philosophes avaient d'ailleurs donné l'exemple en important des mathématiques, non certes des grandeurs, mais la démarche axiomatique elle-même, le cas de Spinoza étant le plus célèbre.
Les retombées des mathématiques dans le domaine des techniques ne sont pas moindres. Depuis la mesure des terrains jusqu'au calcul des trajectoires spatiales, du décompte des troupeaux aux techniques de sondage d'opinion, elles sont présentes dans toutes les activités par lesquelles les hommes s'efforcent de maîtriser la nature et la société. Les moyens informatiques n'ont fait que démultiplier les possibilités de calcul. Le domaine des statistiques, qui doit brasser d'énormes quantités de chiffres, est un de ceux qui en profitent pleinement.
Les thèmes de recherche
Les questions relatives aux fondements des mathématiques ont occupé le devant de la scène pendant les premières décennies du xxe s. On a tendance, depuis, à les laisser aux logiciens. Mais à aucun moment elles n'ont constitué plus qu'une petite partie de la recherche. Les moteurs de celle-ci sont des problèmes, tantôt vastes, tantôt d'un intérêt minuscule à première vue : certains viennent des mathématiques elles-mêmes, d'autres sont posés par les sciences et les techniques.
Un grand thème de recherche, pour se limiter à un exemple, est celui de la complexité, qui porte sur les méthodes de calcul en rapport avec les capacités des machines. Parmi les petits thèmes, la démonstration du théorème de Fermat a reçu une solution satisfaisante au bout de trois siècles et demi d'efforts passionnés. D'autres, comme la conjecture de Goldbach – tout nombre pair est la somme de deux nombres premiers – ou la nature de la constante d'Euler, continuent de jouer leur rôle de défi et celui de prétexte à développer des nouveautés.
