Euclide
Mathématicien de la Grèce antique.
Il existe très peu d'éléments avérés de la biographie d'Euclide. Selon le commentateur Proclus, il aurait vécu au iiie s. avant J.-C. à Alexandrie et serait lié à l'école mathématique du Musée.
1. Les Éléments, un monument des mathématiques
Son œuvre est couronnée par les Éléments, vaste synthèse des mathématiques grecques de l'époque classique. Euclide y déduit des propositions de plus en plus complexes de quelques définitions, postulats (hypothèses pouvant être niées sans contradiction) et axiomes, notions communes évidentes, dont la plus célèbre est l'axiome ou postulat qui porte son nom et selon lequel, par un point du plan, on ne peut mener qu'une parallèle à une droite donnée. La formulation explicite des postulats note la volonté d'Euclide de faire abstraction de la réalité sensible et marque la première apparition de la méthode axiomatique.
Par la rigueur de sa charpente logique, par le choix judicieux des notions de base et par la clarté de ses démonstrations, les Éléments est un ouvrage qui a séduit les mathématiciens de tout temps et leur a servi de modèle pendant plus de deux millénaires.
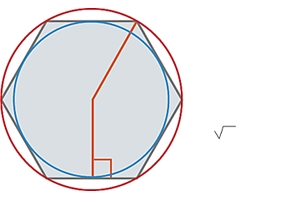
L'ensemble comprend 13 livres, auxquels on en joint deux autres, plus tardifs, attribués à Hypsiclès. On ignore si les 13 premiers sont l'oeuvre d'un seul homme ou d'une école groupée autour d'Euclide. Les quatre premiers livres sont consacrés à la géométrie plane et étudient les propriétés fondamentales des figures polygonales et circulaires (→ géométrie euclidienne).
Le livre II pose les fondements de ce qu'on a appelé l'algèbre géométrique ; toutes les quantités y sont représentées géométriquement et toutes les opérations y sont effectuées géométriquement, c'est-à-dire à l'aide de construction à la règle et au compas.
Le livre V, d'une complexité plus élevée, est parfois attribué à Eudoxe de Cnide. Exposé de la théorie des rapports et des proportions, il fonde la théorie de la mesure des grandeurs. Cette théorie des rapports est appliquée dans le livre VI à la géométrie plane et en particulier aux figures semblables, et, dans les livres VII, VIII et IX, arithmétiques, aux nombres entiers. Le livre X, très subtil, classifie les nombres irrationnels et les derniers livres traitent de la géométrie dans l'espace.
2. Les autres œuvres d'Euclide
Euclide est également l'auteur des Données, sorte de complément des Éléments, des Porismes (corollaires), de la Division du canon sur les proportions musicales, d'une Optique et d'ouvrages perdus sur les sections coniques et la division des aires.