statistique
(allemand Statistik)

STATISTIQUE
Le besoin de posséder des données chiffrées sur la population et ses conditions matérielles d'existence a dû se faire sentir dès que se sont établies des sociétés humaines organisées : on en trouve des traces dans l'Antiquité en Chine, en Égypte, en Grèce, puis avec les recensements ordonnés par Rome, les relevés réalisés sur l'ordre de Charlemagne ou de Guillaume le Conquérant et, enfin, les inventaires royaux exécutés sous l'impulsion de Sully, de Colbert, de Vauban.
Au xviie s. se dessinent les concepts relatifs aux bases et aux moyens des études statistiques, avec le développement de la théorie des probabilités.
Le xixe siècle
Laplace, en 1812, met en évidence les avantages que l'on peut tirer des probabilités dans l'étude des phénomènes naturels, dont les causes sont trop complexes pour qu'on puisse les connaître toutes et les analyser une à une. A. Quételet étend le champ d'application de la méthode à l'étude anthropométrique, psychologique et sociale des êtres humains. À la suite de ces travaux et de ceux de F. Galton, K. Pearson fonde la biostatistique, prolongée maintenant dans le domaine de l'expérimentation thérapeutique. La liaison entre l'observation statistique et l'économie aboutit à la création de l'économétrie. En physique, les travaux de J. C. Maxwell, conduisant à la théorie cinétique des gaz, sont le point de départ de la mécanique statistique. En sciences humaines, les études de C. Spearman sur le comportement des individus, développées par la suite en psychologie appliquée, humaine et animale, conduisent aux méthodes de l'analyse factorielle.
Le xxe siècle
La méthode statistique s'est révélée un auxiliaire indispensable pour la gestion des entreprises : études de marché, contrôle budgétaire, gestion des stocks. Prolongée par la théorie des jeux et la théorie de la décision, elle a donné naissance aux méthodes de la recherche opérationnelle.
Parmi les travaux des dernières décennies, on peut citer, entre autres, ceux de I. Fisher sur la théorie des tests et celle de l'estimation, nés de recherches empiriques sur l'application de la méthode des sondages. Le développement de l'informatique a en outre permis de mettre en œuvre de nouvelles méthodes de statistique descriptive applicables à de grands tableaux de données, méthodes regroupées sous le nom d'analyse des données.
La méthode statistique
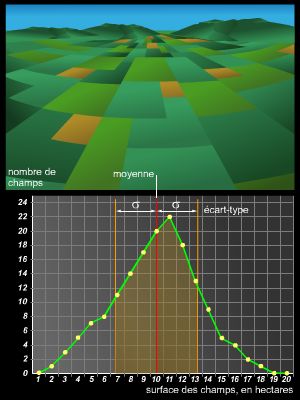
Un travail statistique comporte plusieurs phases. La première consiste à définir les unités statistiques sur lesquelles on va opérer (caractères, nomenclatures, etc.). Dans la deuxième phase, on procède au recueil des données (échantillonnage, mesures, enquêtes par questionnaires, etc.). Dans la troisième phase (statistique descriptive), on présente ces données sous forme de tableaux, de courbes ou de graphiques, qui contiennent toute l'information. On réduit généralement les données en les remplaçant par des courbes plus parlantes (histogrammes), des diagrammes en bâton ou par un petit nombre de paramètres, les uns caractérisant la tendance centrale (moyenne, médiane, mode), les autres la dispersion (quantiles, écart, variance, écart-type, moment, étendue).
Dans la statistique classique (inférence statistique), on essaie ensuite à l'aide de ces paramètres de rattacher les observations à un modèle ou à une loi statistique (binomiale, normale, etc.) ; cela conduit, dans le cas où l'on a procédé à un échantillonnage dans la population étudiée, aux problèmes de l'estimation des paramètres. Pour tirer des conclusions à partir d'un échantillon, il faut faire une hypothèse sur la population totale et porter un jugement sur sa valeur : c'est l'objet des tests d'hypothèse. Enfin, lorsque plusieurs caractères sont déterminés simultanément, on peut chercher s'il existe des liaisons entre eux : liaison fonctionnelle, indépendance totale ou liaison stochastique (corrélation).





