électron

(anglais electron, de electric et anion)

Particule fondamentale portant l'unité naturelle de charge électrique et appartenant à la classe des leptons.

Pour la physique, l'électron est l'objet théorique par excellence. C'est à son propos qu'ont été élaborées la plupart des théories importantes du xx^e s., à commencer par la physique quantique. La physique atomique et moléculaire est essentiellement une physique des électrons. La chimie étudie la formation et la transformation des molécules, c'est-à-dire les transferts d'électrons d'un atome à un autre. La physique de l'état solide s'intéresse à la cohésion de la matière, assurée par les électrons. Plusieurs technologies ont spécifiquement l'électron pour matériau : électronique, informatique, applications médicales des faisceaux d'électrons, etc.

L'électron est l'un des plus importants constituants universels de la matière, dont toutes les propriétés macroscopiques sont, d'une façon ou d'une autre, liées à ses caractéristiques.

1. La découverte de l'électron

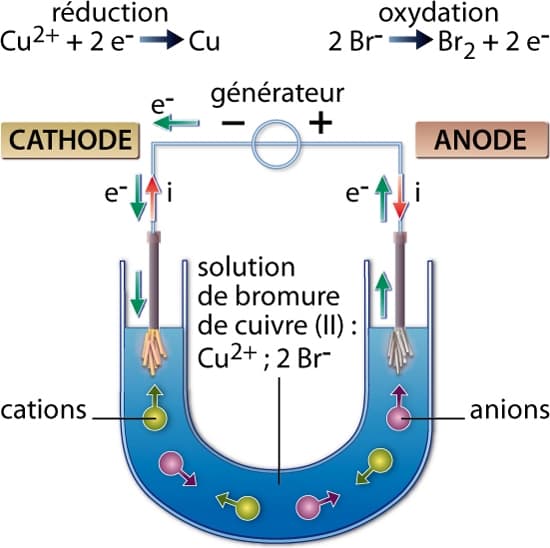
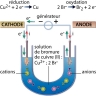
L'étude de l'électrolyse apporta la première preuve expérimentale de l'hypothèse l’existence de grains matériels composant le « fluide électrique ». Diverses mesures effectuées vers les années 1880 montrèrent que la quantité d'électricité nécessaire pour dissocier une mole de n'importe quel corps est un multiple entier d'une même quantité. Le mot « électron » fut inventé en 1891 par l’Irlandais George Stoney pour désigner d'abord la quantité élémentaire d'électricité, puis la particule porteuse de cette quantité elle-même.

Pour en savoir plus, voir l'article électricité.

L'étude des décharges électriques dans des gaz raréfiés (à basse pression) imposa définitivement l'existence de l'électron. Celles-ci s'accompagnent de l'émission de « rayons » (les rayons cathodiques) qui rendent fluorescent le verre de l'ampoule. Jean Perrin en 1895 puis Joseph John Thomson en 1897 réussirent à isoler ces rayons et à montrer, d'abord, qu'ils étaient porteurs d'une charge négative, puis qu'ils étaient effectivement constitués de particules matérielles chargées, dont Thomson mesura la vitesse et le rapport e_e /m_e de leur charge e à leur masse m_e. Quant à la détermination de la charge élémentaire e elle-même, ce fut l'œuvre des vingt années qui suivirent ; en 1910, Robert Millikan, au terme d'une expérience particulièrement délicate, établit la valeur de e avec une précision extraordinaire pour l'époque.

2. L’électron, constituant fondamental de l’atome

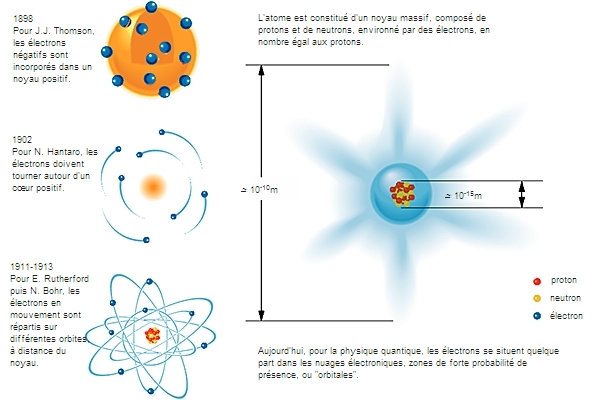
L'idée d'une structure complexe de l'atome était tellement révolutionnaire au début du xx^e s. que, pour l'imaginer, on fit appel à des « modèles classiques » de la physique. Une fois les caractères des ions positifs et de l'électron maîtrisés, la question de leur coexistence dans l'atome intrigua les physiciens.

2.1. Les premières tentatives de modélisation de l'atome

Comme il n'était pas possible d'observer la structure atomique, il fallait concevoir un « modèle » qui permît de comprendre des phénomènes physiques que l'on pensait être corrélés à une telle structure. Pour Hantaro Nagaoka (1904), le critère principal, emprunté aux phénomènes chimiques, devait expliquer la formation des molécules à partir des atomes. Il imaginait l'atome comme une structure stable, semblable à la planète Saturne : il plaçait les électrons sur les anneaux et assimilait la planète au noyau. Tout en acceptant que le critère de comparaison devait être fourni par la chimie, J. J. Thomson pensait, au contraire, que les électrons circulaient à l'intérieur d'une sphère dont la surface était chargée positivement.

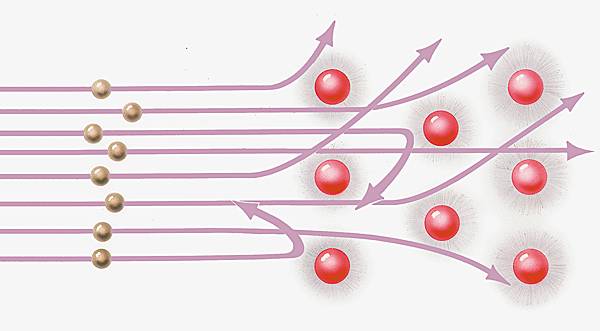
Ce modèle n'était plus viable dès qu'on prenait en compte un autre phénomène : la diffusion des particules α, émises par désintégration radioactive du polonium, à travers une feuille de platine, qu'Ernest Rutherford avait observée, laissait penser que la charge atomique positive était concentrée en un point car quelques particules α étaient fortement déviées. Pour que les résultats expérimentaux soient compatibles avec le modèle planétaire, il fallait considérer que la charge positive était concentrée au centre de l'atome. Vers 1911, ce modèle semble satisfaire et la chimie et la physique, même s'il est toujours impossible de montrer sa compatibilité avec l'ensemble des lois de cette dernière. L'atome ressemble au Système solaire : le noyau positif est au centre, et les électrons se déplacent sur des orbites à l'extérieur du noyau. Cependant, les électrons, en tournant, doivent émettre de l'énergie. Selon un tel modèle, encore grossier, ils s'approcheraient du noyau jusqu'à être détruits par combinaison des charges positive et négative, rendant l'atome fortement instable. Après une dizaine d'années de recherches, malgré cette objection de fond, des certitudes étaient partagées par les chercheurs : la concentration de la masse et de la charge positive dans le noyau, les électrons étant situés à l'extérieur du noyau ; autre certitude : la stabilité du modèle supposé, dit de Rutherford. Mais, pour comprendre la structure de l'atome, il fallait une clé supplémentaire.

2.2. Structure atomique et spectroscopie

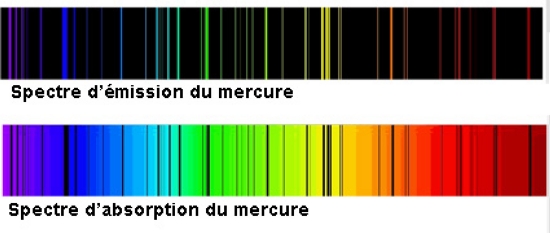
Ce fut la grande intuition du Danois Niels Bohr que de corréler, en 1913, la structure des atomes avec leurs spectres. Un spectre est l'enregistrement de l'énergie absorbée ou émise par les atomes. Bien que différents pour chaque élément, les spectres ont un aspect semblable : des lignes espacées différemment entre elles, correspondant aux valeurs d'énergie absorbée ou émise. Cette structure régulière se prête bien à la traduction en formules du type « la différence d'énergie entre deux lignes est égale à un multiple entier d'une même quantité ». Or une nouvelle conception s'affirmait en physique depuis le début du siècle : l'énergie est aussi concevable comme constituée de petits grains, unités appelées au début « quanta de lumière » (Einstein, 1905), et depuis 1924 « photons ».

L'énergie des spectres correspondait-elle également à des multiples entiers du quantum ? Pouvait-on corréler l'absorption ou l'émission d'énergie avec le déplacement des électrons à l'intérieur des atomes ? Y parvenir pouvait permettre d'évaluer l'énergie correspondant à un électron dans un atome. Le modèle de l'atome calqué sur la structure planétaire paraissait donc se préciser : les électrons évoluent, de manière stable, sur des orbites qui sont les seules positions possibles. Un électron peut passer d'une orbite à une autre par absorption ou émission d'énergie, cette énergie étant toujours un multiple entier du quantum.

Pour calculer les différentes orbites possibles, on fit appel aux théorèmes de la mécanique. On imagina ainsi des orbites elliptiques ; celles-ci pouvaient être inclinées différemment par rapport à un axe. Il était dès lors possible de distinguer les électrons en leur attribuant des paramètres : les deux premiers correspondaient aux deux axes de l'ellipse et le troisième, à l'inclinaison par rapport à l'axe perpendiculaire à la première orbite et passant par le noyau. Cette construction avait été rendue possible par la confrontation entre données spectroscopiques et déductions théoriques à partir des modèles mécaniques. Cette méthodologie allait pourtant achopper bientôt sur une difficulté majeure.

2.3. Le modèle quantique de l’électron

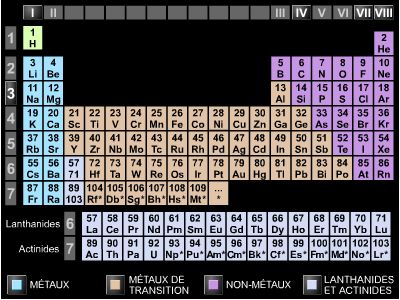
La diversité des éléments chimiques, dans le cadre du modèle des atomes planétaires, était expliquée par le fait que chaque élément est caractérisé par un nombre donné d'électrons (correspondant au numéro atomique), ceux-ci se disposant sur les orbites possibles du point de vue énergétique. Ainsi, chaque électron a d'abord été caractérisé par trois nombres entiers, dits nombres quantiques, obtenus par l'étude géométrique des orbites. On établissait aussi de cette manière l'interdépendance de ces nombres entre eux.

Le premier, le nombre quantique principal, généralement indiqué par n, est relié au niveau énergétique et indique l'axe principal de l'ellipse ; le deuxième, le nombre quantique azimutal, indiqué par l, peut assumer les valeurs 0 à (n − 1), et indique l'excentricité de l'orbite ; le troisième, le nombre quantique magnétique, indiqué par m, peut avoir les valeurs de −l à +l et représente l'inclinaison spatiale de l'orbite.

Or Wolfgang Pauli, à partir d'une analyse pointilleuse des données spectroscopiques, montra en 1924-1925 que la seule manière d'établir une correspondance entre l'ensemble des lignes observées pour un atome et les nombres quantiques était d'ajouter un quatrième nombre quantique (le spin s) en lui imposant uniquement deux valeurs : +1/2 ou −1/2. Certes, peu de temps après, George E. Uhlenbeck et Samuel A. Goudsmit réussirent à montrer, pour l'hydrogène, que ce nombre supplémentaire pouvait correspondre au moment cinétique propre de rotation de l'électron, appelé spin. Cette représentation mécanique constitue le dernier effort pour rester dans le cadre des anciens modèles. En effet, face à la multiplicité des modèles et en l'absence de critères physiques pour les départager, les physiciens furent convaincus que la structure des atomes allait devoir être repensée entièrement.

2.4. Le modèle ondulatoire de l’électron

Deux voies furent suivies en même temps : des chercheurs, abandonnant l'image trop réaliste du modèle planétaire, raisonnèrent sur les seules grandeurs observables et mesurables, d'origine mécanique comme la position et la quantité de mouvement ; d'autres mirent l'accent sur la nature ondulatoire de l'électron.

2.4.1. L’électron selon Louis de Broglie

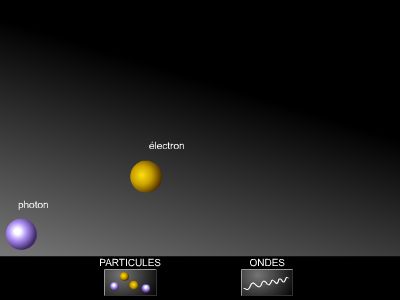
En 1924, Louis de Broglie montrait que les propriétés corpusculaires des électrons ont une contrepartie ondulatoire avec, comme relation fondamentale, la longueur d'onde λ = h /p, où h est la constante de Planck et p la quantité de mouvement de l'électron. On savait depuis les travaux de Hamilton, au milieu du xix^e s., qu'un ensemble de corpuscules pouvait être représenté, mathématiquement, comme une onde. Cependant, s'agissait-il d'une pure possibilité mathématique ou d'une réelle capacité de l'électron à produire des phénomènes typiques de la théorie ondulatoire ? L'un de ceux-ci, le plus caractéristique même, correspond aux figures de diffraction. Ainsi, les expériences de Davisson et Germer, qui enregistrèrent en 1927 la figure de diffraction d'un faisceau d'électrons sur un mince cristal de zinc, furent considérées comme la preuve irréfutable de la double nature de l'électron : ondulatoire et corpusculaire.

L'électron présentait alors une analogie parfaite avec la lumière, qui peut être définie comme composée de photons, de spin nul, et comme une onde. Seule la valeur du spin – entier pour le photon et demi-entier pour l'électron – les départage ; ainsi, la réalité corpusculaire subatomique a comme grandeur typique le spin.

Cette conception de l'électron comme onde eut des prolongements techniques extrêmement importants. Par analogie avec le microscope optique, il a été possible de concevoir un microscope électronique (mettant en œuvre une source d'électrons, un réseau de diffraction, un système d'enregistrement – plaque photographique ou écran fluorescent – sur lequel est enregistré l'objet agrandi) dont la capacité d'agrandissement dépasse les 100 000 fois.

2.4.2. L’électron selon Erwin Schrödinger

Erwin Schrödinger décrivit l'électron comme une suite de fonctions ondulatoires. De plus, il obtenait les mêmes valeurs de l'énergie que celles que l'on calculait avec le modèle corpusculaire. Enfin, il était possible de passer de l'une à l'autre description car, du point de vue mathématique, elles sont équivalentes.

De ce fait, les physiciens se trouvaient confrontés à un problème supplémentaire : faut-il penser qu'à chaque corpuscule est étroitement associée une onde, ou que les descriptions ondulatoire et corpusculaire sont deux manières, complémentaires, de décrire une même réalité qui nous échappe ? Pour résumer, fallait-il accentuer l'analogie de ce problème avec ceux qui se posent dans d'autres domaines de la physique, comme l'optique ou l'acoustique, où cohabitent plusieurs points de vue, ou tenir ces résultats pour provisoires, en attendant une nouvelle théorie qui éliminerait le caractère de complémentarité associé à la nécessité de faire appel à deux visions ? Le débat est encore ouvert en physique, et pour l'instant il n'existe pas de théorie de remplacement.

La seule certitude des physiciens est que l'électron se situe à l'intérieur de l'atome, et qu'on ne peut indiquer que sa probabilité de présence dans ce confinement. Pour connaître la position de l'électron, il faut expérimenter ; or toute expérience perturbe le système de telle sorte qu'on ne sait plus où se situe l'électron après l'expérience. De plus, certaines grandeurs physiques mesurables sont liées entre elles de telle façon que, si l'on augmente la précision de la mesure de l'une, on réduit d'autant la précision de l'autre : il y a une indétermination fondamentale dans notre connaissance expérimentale de ces grandeurs. L'étude de l'électron aboutit donc à ces conclusions :
– toute description théorique revient à se donner des probabilités d'événements ;
– l'expérimentation perturbe tout système soumis à mesure ;
– si, au cours d'une même expérience, on veut évaluer en même temps des grandeurs liées, la précision de chaque mesure ne peut pas être arbitrairement élevée : plus on soigne l'un des paramètres, moins on obtient de précision sur l'autre ; la précision est donc toujours limitée.

3. L'électron dans les solides

• 
• 

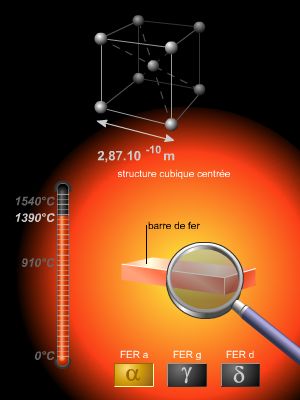
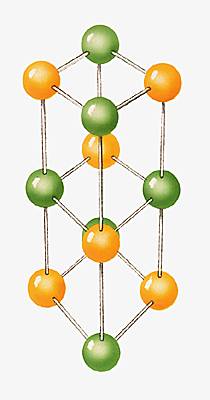
Qu'apportait cette nouvelle vision à la connaissance des métaux ? D'énormes progrès avaient été réalisés dans la connaissance de leur structure. Les rayons X étant caractérisés par une faible longueur d'onde, la structure atomique d'un métal constitue un réseau naturel de diffraction pour cette « lumière », qui traverse la matière. Ainsi, en observant les réseaux de diffraction, on pouvait, par des calculs numériques extrêmement complexes, parvenir à déterminer la structure atomique. La cristallographie avait déjà habitué les savants à reconnaître dans les cristaux la présence de structures géométriques régulières ; cette connaissance fut étendue aux métaux, qui révèlent à l'échelle atomique une régularité non perceptible au niveau macroscopique. De plus, la diffraction des rayons X permettait d'apprécier la distance entre les lignes du réseau, et donc de mesurer la distance entre atomes. Ces valeurs, confrontées aux dimensions que l'on pouvait calculer à partir des modèles atomiques, montraient que la distance entre atomes d'un métal est telle qu'il faut supposer que les couches électroniques les plus externes sont en contact. La structure d'un métal est donc bien plus compacte qu'on ne l'imaginait. On conclut que les électrons de valence se déplacent dans un champ électrique intense, fort complexe, créé par les noyaux et les autres électrons atomiques. L'hypothèse des électrons libres relevait donc de la fiction. Mais comment oublier que, qualitativement au moins, un accord remarquable existait entre ce modèle et les données de l'expérience ?

3.1. L'approche chimique

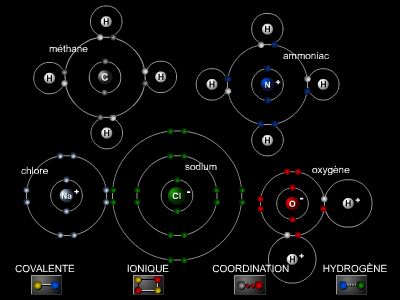
La clé de cette énigme va être fournie par la compréhension de la liaison chimique. Les couches électroniques externes étant très proches, au point de se toucher, on suppose qu'il se produit un phénomène analogue à la formation d'une molécule à partir des atomes. L'analogie est presque parfaite : comme les molécules, les atomes gardent leur individualité tout en formant un nouveau composé dont l'action est spécifique ; dans le métal, les atomes gardent aussi leur individualité, et leur assemblage manifeste des caractères physico-chimiques propres.

3.1.1. Les électrons dans la liaison ionique

La cohésion moléculaire est considérée comme le résultat de l'attraction électrostatique entre ions de charge opposée. C'est le cas de la plupart des sels qui, en solution, se dissocient en ions. En général, ces molécules sont composées d'atomes de structure électronique fort dissemblable – on dit aussi qu'ils sont situés dans les cases extrêmes du tableau de Mendeleïev. L'un d'entre eux tend à se séparer de son ou de ses électrons externes pour atteindre une configuration électronique stable (huit électrons sur la couche externe), l'autre tend à s'annexer le ou les autres électrons, pour la même raison.

3.1.2. Les électrons dans la liaison covalente

Pour atteindre une configuration électronique stable, les atomes adoptent une solution de compromis : ils mettent en commun les électrons externes. C'est, par exemple, le cas de la liaison entre deux atomes de carbone, courante dans les composés organiques. Il faut l'imaginer comme un nuage électronique entourant les deux noyaux, qui se placent à une distance telle qu'elle correspond à un minimum de l'énergie pour l'ensemble du système.

3.2. Électrons et nuage électronique

Transposée au niveau des solides, l'image du nuage électronique implique le partage des électrons entre tous les atomes ; or cette image est fort semblable à l'hypothèse « ancienne » des électrons libres dans un métal, son réalisme naïf en moins. Pour la tester, il fallait faire appel aux méthodes de calcul de la mécanique quantique. Le point crucial est donc de résoudre ce problème du point de vue mathématique : il s'agit d'écrire une équation pour N corps en mouvement, N étant une valeur très grande correspondant aux électrons qui font partie de la liaison. Ce problème est soluble uniquement par des méthodes mathématiques approchées et il faut faire des hypothèses physiques « raisonnables » pour en simplifier la résolution.

L'hypothèse suivante s'est révélée féconde : les électrons gardant leur individualité, on va les considérer isolément. Il s'agit donc d'écrire l'équation du mouvement de l'un d'entre eux en présence d'un champ électrique issu des noyaux disposés selon les nœuds du réseau cristallin, champ auquel font écran les autres électrons. La nature symétrique de ce champ complexe permet d'introduire des simplifications ; il s'agit ensuite de l'évaluer raisonnablement. Si un composé ou un métal est stable, cela veut dire que son énergie est inférieure à la somme de l'énergie des atomes le composant. Transférée sur le plan de la description mathématique, cette idée revient à considérer que les fonctions atomiques qui décrivent l'électron seront sans doute changées, mais pas totalement ; elles peuvent donc constituer un point de départ raisonnable pour résoudre l'équation. Une fois trouvée une première solution, il faut modifier et le champ et les fonctions, puis répéter ce calcul tant que les petits changements apportés ne modifient pas les données importantes que sont les valeurs de l'énergie pour chaque électron dans le métal. Cette longue suite de calculs numériques est aujourd'hui possible grâce aux ordinateurs.

En général, on obtient des solutions du type suivant : les valeurs d'énergie permises au niveau atomique se regroupent dans des ensembles caractérisés par des énergies très proches, qui se confondent en une sorte de zone appelée bande. Ces bandes se distribuent sur une échelle des énergies croissantes ; elles peuvent se recouvrir en partie, ou être séparées par un large gap (écart) d'énergie. Partant de N fonctions atomiques, on obtient N niveaux énergétiques qui se regroupent en bandes. Comme dans la liaison chimique, l'occupation par les électrons des bandes les plus externes devra permettre de comprendre les phénomènes de conduction électrique et thermique. Les électrons s'« empilent » par deux et par fonction, selon le principe de Pauli. On peut alors schématiser ainsi les situations possible  : la bande externe est totalement remplie d'électrons, ou elle l'est partiellement ; la bande immédiatement supérieure, vide d'électrons, recouvre partiellement ou pas du tout la bande dernièrement occupée.

3.3. Électrons et propriétés des solides

Ce simple schéma des situations possibles du point de vue énergétique permet de rendre compte de ce qui paraissait inexplicable dans l'ancienne théorie de l'électron libre. Un électron peut être considéré comme libre d'occuper n'importe quel niveau d'énergie à l'intérieur d'une bande. Si deux bandes se superposent, il peut passer aisément de l'une à l'autre.

Théoriquement, ces mini-sauts demandent toujours une dépense énergétique, mais elle peut être considérée comme suffisamment faible pour que les sauts adviennent. Cette mobilité rend bien compte des propriétés conductrices des solides. Un isolant électrique est un solide où la dernière bande est complètement remplie et la bande vide, immédiatement supérieure, nettement séparée ; pour qu'il y ait mobilité, il faudrait fournir suffisamment d'énergie pour exciter les électrons sur la bande libre. Un bon conducteur présente la configuration inverse : si les deux dernières bandes se recouvrent, il suffit de peu d'énergie pour redistribuer les électrons. Un mauvais conducteur est un solide dont la distance entre la dernière bande remplie et la bande immédiatement supérieure n'est pas très grande : il suffit de peu d'énergie pour le rendre faiblement conducteur. Un tel modèle permet aussi d'expliquer pourquoi la chaleur spécifique des solides, dans les limites de validité de la loi de Dulong et Petit, est une constante. Dans le cas des mauvais conducteurs, la contribution électronique peut être considérée comme nulle ; dans les autres cas, la mobilité électronique est telle qu'elle ne change pas considérablement par l'augmentation de la température dans des limites définies. Dans les deux cas, la contribution des électrons à la chaleur spécifique est négligeable.

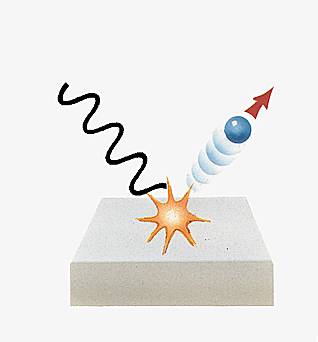
Cette approche a en outre le mérite de relier aux modes de distribution électronique d'autres faits physiques, comme l'émission thermo-ionique, à l'origine de l'électronique classique, celle à tubes. On sait qu'en chauffant un métal il se produit une émission d'électrons. Cela signifie que ces électrons ont une énergie cinétique telle qu'ils dépassent la barrière représentée par la surface du métal. Ainsi, la surface devient du point de vue physique une discontinuité fondamentale dans le potentiel. Si cette analyse est bonne, on doit pouvoir expliquer, par analogie, l'effet photoélectrique, dans lequel l'énergie est fournie par le rayonnement incident. Ainsi que l'avait déjà observé Einstein, il faut un rayonnement d'une certaine longueur d'onde pour faire s’échapper des électrons d’un matériau. De ce fait, effets thermoélectrique et photoélectrique relèvent de la même explication.

L'électron décrit par les équations de la mécanique quantique perd son image de particule à laquelle sont associées une masse et une charge ; en revanche, il permet de mieux maîtriser et expliquer les phénomènes complexes propres aux solides.