hyperbole

(grec huperbolê, excès)

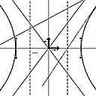
Ensemble des points d'un plan, dont la valeur absolue de la différence des distances à deux points fixes (foyers) de ce plan est constante.

GÉOMÉTRIE

L'hyperbole a deux axes de symétrie : la droite joignant les foyers F et F′ (axe focal), et la médiatrice de [FF′] ; elle a deux asymptotes sécantes au milieu de [FF′], centre de symétrie. À chaque foyer F ou F′ correspond une droite D ou D′, appelée directrice, telle que le rapport des distances d'un point de l'hyperbole au foyer et à la directrice est une constante, e (e>1), appelée excentricité. En prenant comme axes de coordonnées les deux axes, l'équation de l'hyperbole est 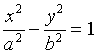, en prenant les asymptotes : xy = k. Celles-ci ont pour équations : y = bx/a et y = −bx/a. Pour a = b l'hyperbole est dite équilatère. En posant c² = a² + b², on a les relations : e = c/a et FF′ = 2c.