fonction

(latin functio, -onis, de fungi, s'acquitter)

Relation qui, à chaque élément de son ensemble de départ, associe au plus une image.

MATHÉMATIQUES

• 
• 
• 

La notion de « fonction » ne s'est d'abord appliquée qu'aux fonctions réelles de la variable réelle. Les notations sont alors

.

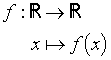
On distingue les fonctions rationnelles telles que les fonctions affines, les fonctions polynômes, etc. ; leurs images ne sont définies qu'à l'aide des quatre opérations (+, −, × et :) ; les fonctions irrationnelles où, pour les images, apparaissent des nombres irrationnels. Ces deux catégories sont des fonctions algébriques. Les suivantes sont des fonctions transcendantes : les fonctions exponentielles ; les fonctions circulaires ; les fonctions hyperboliques.

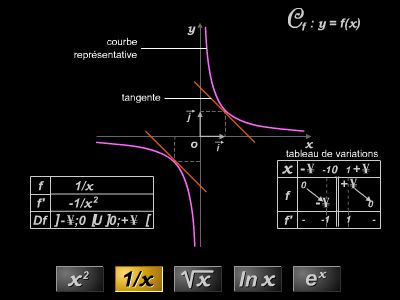
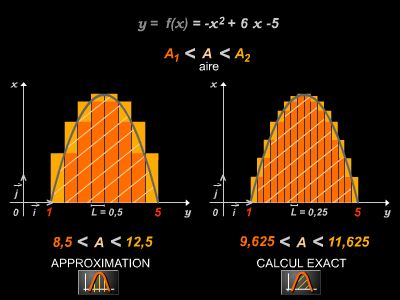
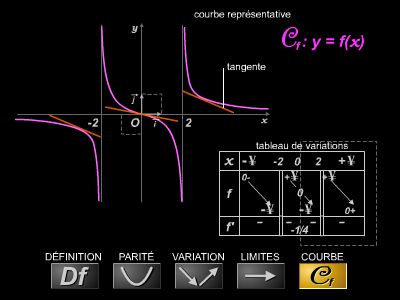
L'étude d'une fonction numérique consiste à déterminer son domaine de définition, les limites de la fonction aux bornes des intervalles formant ce domaine, les intervalles où la fonction est soit croissante, soit décroissante. Ces résultats sont consignés dans un tableau ; en général, on effectue une représentation graphique de la fonction étudiée.

Fonction exponentielle de base a

Fonction qui, lorsqu'elle est définie sur ℝ, est obtenue comme réciproque de la fonction logarithme de base a. (Notation : exp_a.)

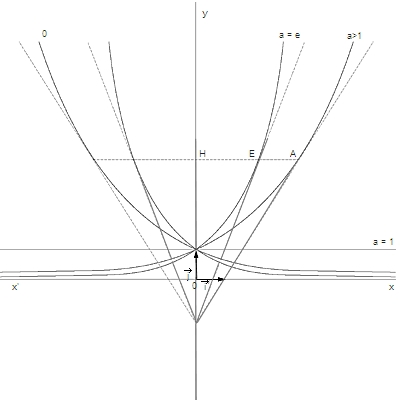
Les fonctions exponentielles de base a définies sur ℝ doivent leurs propriétés à celles des fonctions logarithmes de base a. Ainsi, si a >1, log_a est une bijection continue et croissante de ℝ^+* dans ℝ : sa fonction réciproque exp_a est donc une bijection continue et croissante de ℝ dans ℝ^+*. De même si 0 < a < 1, log_a est une bijection continue et décroissante de ℝ dans ℝ^+* ; sa fonction réciproque, exp_a est donc une bijection continue et décroissante de ℝ dans ℝ^+*. Ces fonctions sont des isomorphismes de (ℝ, +) sur le groupe multiplicatif (ℝ^+*, ×) : en particulier
∀(x, y) ∈ ℝ², exp_a (x + y) = exp_a x. exp_a y ;
exp_a 0 = 1 ; exp_a 1 = a ;
∀x ∈ ℝ, exp_a(−x) = 1/exp_a x
et, par conséquent,
∀(r, x) ∈ ℚ × ℝ, exp_a rx = (exp_a x)^r.
Par rapport à ce qui se passe dans ℚ, on est conduit à poser ∀ x ∈ ℝ, ∀ a ∈ ℝ^+*, exp_a x = a^x.

On obtient aussi :
exp_a x = a^x = e^{x. ln a},
∀ (x, y) ∈ ℝ², ∀ a ∈ ℝ^+* ;
a^x. a^y = a^{x + y} et (a^x)^y = a^{x. y}.

La dérivée de exp_a est alors la fonction
x ↦ a^{x.ln a}.

La fonction exponentielle (exp) est l'application x ↦ e^x, et sa fonction dérivée l'application x ↦ e^x ; elles sont donc égales.

Fonction homographique

Fonction définie de ℂ dans par :
si z ≠ ∞ et
et . (On précise fonction homographique propre lorsque ad − bc ≠ 0, f étant alors bijective, ou fonction homographique impropre lorsque ad − bc = 0, f étant alors une fonction constante.)

Si c = 0, f est une similitude ou une translation ; si c ≠ 0, la fonction homographique propre est composée d'un nombre fini d'applications prises parmi les types suivants : translation (z ↦ z + h), similitude (z ↦ k. z), inversion-symétrie (z ↦ z⁻¹). Les applications homographiques conservent le birapport.

Fonction positivement homogène de degré n

Fonction numérique définie sur la partie D d'un espace vectoriel E, vérifiant :
1° ∀ α ∈ ℝ⁺, si x ∈ D, alors α. x ∈ D ;
2° ∀ α ∈ ℝ⁺, ∀ x ∈ D, f(α. x) = αⁿ. f(x). (On dit aussi plus simplement que f est homogène.)

Le degré d'homogénéité d'une fonction est un nombre rationnel. Si f est homogène de degré n sur l'espace vectoriel ℝ^p, chacune de ses dérivées partielles, si elle existe, est homogène de degré n − 1. Le théorème d'Euler donne une propriété des fonctions homogènes.

Fonction analytique de n variables

fonction f à valeurs réelles ou complexes, définie sur un ouvert D et telle que f est développable en série entière en tout point de D.

Propriétés des fonctions analytiques

Pour une fonction analytique, il existe en tout point x₀ de D un réel ρ(x₀)>0 et une série , de rayon de convergence supérieur ou égal à ρ(x₀), telle que 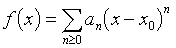pour | x − x₀ | < ρ(x₀). Une fonction analytique dans D est indéfiniment dérivable dans D et ses dérivées successives sont analytiques dans D.