cycloïde
(grec kukloeidês, circulaire)

Roulette engendrée par un point situé sur un cercle qui roule sur une droite. (Synonyme : trochoïde.)
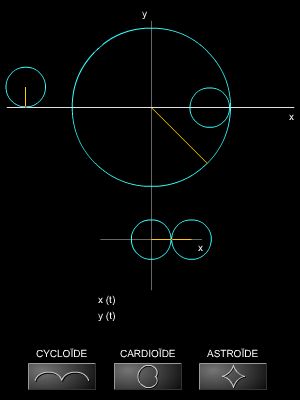
La cycloïde fut la courbe la plus étudiée dans la première moitié du xviie s. ; elle a permis aux mathématiciens de mettre au point les techniques anticipant la différentiation et l'intégration : Roberval en fit la quadrature et en construisit la tangente, pour laquelle Descartes, Fermat donnèrent d'autres solutions. Si R est le rayon du cercle qui roule, une équation paramétrique de la cycloïde est f(t) :
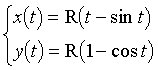
.





