circuit électrique

Les caractéristiques des circuits électriques

Un circuit électrique (ou réseau) comporte des éléments actifs, ou sources d'énergie (générateurs et récepteurs), et des éléments passifs pouvant être représentés par un certain nombre, soit fini (circuit à constantes localisées), soit infini (circuit à constantes réparties) d'éléments idéaux caractérisés par l'une des 4 grandeurs : résistance R, capacité C, inductance propre (ou self-inductance) L, inductance mutuelle M. La loi d'Ohm permet d'exprimer la tension v(t), différence de potentiel aux bornes de l'élément, en fonction du courant i(t) qui le parcourt.

Dans un circuit maillé, on appelle :
branche, une suite d'éléments connectés en série et traversés par le même courant ;
nœud, le point de concours de plusieurs branches ;
boucle, tout ensemble de branches formant un parcours fermé ;
arbre, tout ensemble connexe de branches joignant tous les nœuds sans former de boucles ;
liaison d'un arbre, toute branche du réseau n'appartenant pas à cet arbre ;
coarbre, l'ensemble des liaisons d'un arbre ;
maille, la boucle formée par l'adjonction d'une liaison à un arbre.

Les principales lois des courants

Les courants sont reliés par les deux lois de Kirchhoff : selon la loi des nœuds, la somme algébrique des courants aboutissant à un nœud est nulle et, selon la loi des boucles, la somme algébrique des tensions aux bornes des branches constituant une boucle est nulle.

En régime continu, une branche quelconque bb′ est caractérisée par sa force électromotrice (f.é.m.) équivalente E et sa résistance équivalente R ; en désignant par V la tension entre b et b′ et par I le courant passant de b à b′, la loi d'Ohm s'écrit V = + E + RI, les signes + et − dépendant du signe de la f.é.m.

En régime harmonique, les tensions et les courants sont des fonctions sinusoïdales du temps de pulsation ω = 2πf.

Les relations entre les valeurs complexes de la tension et du courant s'écrivent, en posant j² = −1 :
pour une résistance R,  ;
pour une capacité C,  ;
pour une inductance L, .

Dans une branche quelconque du réseau caractérisée par sa f. é. m. équivalente et par son impédance complexe , la relation entre la tension complexe 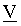et le courant complexe s'écrit .

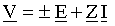L'équation fondamentale du circuit magnétique, déduite du théorème d'Ampère, est la relation d'Hopkinson NI = ℛΦ, expression où NI est la force magnétomotrice du circuit (mesurée en A), Φ le flux d'induction (en Wb), et ℛ la réluctance (en H⁻¹). La formule d'Hopkinson peut se généraliser à tous les circuits magnétiques, quelle que soit leur complexité.