Bertrand, 3^e comte Russell

Philosophe et logicien britannique (Trelleck, pays de Galles, 1872-Penrhyndeudraeth, pays de Galles, 1970).

Un jeune homme seul

Les premières années du philosophe sont marquées par le deuil et le puritanisme : Bertrand Arthur William Russell a deux ans quand meurent sa mère et ses deux sœurs, et quatre ans quand son père disparaît. Il est confié à sa grand-mère. Revoyant sa vie bien des années après dans une œuvre qu'il a intitulée The Autobiography of Bertrand Russell (volume I : 1872-1914 ; volume II : 1914-1944 ; volume III : 1944-1967), publiée à Londres en 1967-1968 et traduite en français en 1968-1970, il raconte ce que fut pour lui cette vie, notamment dans le jardin de sa grand-mère, où il se promenait seul, « laissé à l'état sauvage ». Ce sont les nurses, les gouvernantes allemandes ou suisses qui l'entourent et le grondent. « J'avais en fait une propension peu commune à la conscience du péché. » À onze ans, Russell découvre la géométrie : la passion des mathématiques devient tellement envahissante que sa grand-mère doit limiter les leçons et que l'enfant travaille « en cachette dans sa chambre à coucher, à la lueur d'une bougie ». L'autobiographie de Stuart Mill lui fait penser qu'il n'y a pas de réponse à la question « Qui a créé Dieu ? » : « Et c'est ainsi que je devins athée », conclut-il. En octobre 1890, il est reçu à Trinity College (Cambridge). Sa voie intellectuelle est désormais tracée : ce sera un perpétuel aller et retour entre la morale et la logique.

Cambridge et le mariage

C'est à Cambridge que Russell rencontre tous ceux qui vont devenir ceux qu'il appelle ses « amis intimes » : son maître, Alfred North Whitehead ; Crompton, tout à la fois hostile au socialisme et à l'entreprise privée ; J. M. E. McTaggart, philosophe timide et hégélien intègre. À l'heure du bilan, Russell avouera : « Si Cambridge a beaucoup compté dans ma vie, ce fut par les amis que je m'y suis faits et l'expérience que j'y ai acquise dans la discussion des idées ; en revanche, l'enseignement proprement dit ne m'apporta pratiquement rien. » C'est chez des amis, lors d'un séjour chez son oncle, qu'il rencontre Sydney et Beatrice Webb dont les idées le remuent profondément puis Alys Pearsall Smith, avec qui il se mariera en 1894.

Les débuts dans la vie

En 1894, ses examens terminés, Russell voyage à Paris, puis à Florence, où il découvre l'art ; en 1895, il rentre passer sa maîtrise, puis se rend à Berlin, où il fréquente les socialistes, dont Bebel et le frère de Karl Liebknecht. Il rédige des notes qui vont devenir son premier livre, publié en 1896 sous le titre de German Social Democracy ; mais il a déjà décidé de se consacrer aux mathématiques. L'année suivante, il met en forme son mémoire de maîtrise (An Essay of the Foundations of Geometry), qu'il publie en 1897 à Cambridge ; en 1900 paraît A Critical Exposition of the Philosophy of Leibniz. Sa collaboration avec Whitehead va devenir plus étroite. Il se rend à Paris avec lui et il y rencontre G. Peano (1900). Russell rédige alors The Principles of Mathematics (1903). En 1907, il tente de se présenter aux élections avec dans son programme le vote féminin ; il ne reçoit que quolibets. Il mène ainsi tout de front et fait paraître Philosophical Essays (en 1910) : la même année paraît le premier volume des Principia Mathematica, rédigé avec Whitehead (2^e volume en 1910 ; 3^e volume en 1913). En mars 1911, il rencontre à Paris Ottoline Morrell, dont il s'éprend.

La Première Guerre mondiale

Les opinions de Russell heurtaient déjà depuis longtemps Whitehead ; la guerre précipite la rupture entre les deux hommes. Le pacifisme de Russell s'exprime dès lors avec fermeté et l'oppose à ses anciens amis. Ses pamphlets sont réunis dans Justice in War Time (1916). Sa lutte contre la guerre s'accentue : Russell rédige Principles of Social Reconstruction (1916), dont la parution entraîne son interdiction comme conférencier. En mai 1918, il est condamné à six mois de prison ferme ; il y écrit Introduction to Mathematical Philosophy (1919). À sa sortie de prison, il côtoie de plus près le socialisme (Roads to Freedom, 1918). Il se rend en U.R.S.S. en 1920, et, là encore, son individualisme aristocratique l'emporte et déçoit ses nouveaux amis, qui le rangent désormais parmi les « laquais de la bourgeoisie ». En 1920, Russell part pour la Chine en compagnie de Dora Black, avec qui il se remariera à son retour. En novembre 1921 naît son premier enfant : « J'éprouvai intensément la délivrance d'une passion longtemps contenue, et, durant les dix ans qui ont suivi, mes principaux intérêts furent d'ordre paternel. »

Russell refait le point de sa connaissance en logique avec la publication de The Analysis of Mind en 1921. En 1922 et en 1923, il présente une nouvelle fois sa candidature au Parlement, en préconisant la lutte contre l'impérialisme, l'impôt sur le capital, les réformes de l'enseignement et la reconnaissance politique de l'U.R.S.S. En vain : les électeurs lui préfèrent le candidat conservateur. En 1931, la disparition de son frère aîné le fera héritier du titre : le 3^e comte Russell pourra désormais siéger à la Chambre des lords.

Une tentative pédagogique

Une vingtaine d'enfants fréquente l'école qu'il a fondée avec sa femme en 1927. Les principes reposent sur une éducation sans larmes et sur une morale sans contrainte. Russell se retrouve rapidement avec des élèves qui sont des cas sociaux, qui tourmentent ses propres enfants et qui l'amènent à des méthodes exténuantes de surveillance. En outre, l'échec financier est tel qu'il devra fermer l'école.

En 1935, Russell se sépare de sa seconde femme ; il épousera l'année suivante Patricia Helen Spence, dont il aura un fils.

Russell en Amérique

En 1938, Russell part pour Chicago, où Rudolf Carnap et Charles Morris assistent à ses cours ; puis il est invité au collège de la cité de New York (1940). Ce collège dépend du gouvernement de la cité, dont Russell dira sans ambage que c'était un « satellite du Vatican ». Les ouvrages du philosophe sont déclarés « lubriques, aphrodisiaques et dépourvus de tout ressort moral ». Russell n'en continue pas moins conférences, cours et publications (An Inquiry into Meaning and Truth, 1940), mais il perd son emploi et doit rentrer en Grande-Bretagne en 1944.

Le combattant de la paix

À son retour, Russell enseigne à Trinity College. Il publie A History of Western Philosophy (1945) et reprend ses leçons sur les limites de la connaissance, qu'il résume dans Human Knowledge : its Scope and Limits (1948). Ses conceptions pacifistes se sont radicalisées après la bombe atomique d'Hiroshima. Désormais, sa vie va se dérouler au rythme des marches pacifiques, des conférences et des prises de parole. En juin 1950, il se rend en Australie et, tout en traitant de la guerre froide devant ses auditeurs, observe et condamne la ségrégation raciale entre Australiens anglo-saxons de souche et aborigènes. À la fin de 1950, il se rend à Stockholm pour recevoir le prix Nobel de littérature. En 1952, il divorce de nouveau et épouse Edith Finch. La B.B.C. l'invite à une conférence intitulée « l'Homme en danger », dont il rédige un manifeste destiné à tous les savants du monde. L'intervention de la Grande-Bretagne à Suez le révolte. Russell crée avec d'autres savants la « conférence Pugwash », qui se réunit périodiquement et dont l'influence est grande. En janvier 1958, il participe au lancement de la « Campaign for Nuclear Disarmament » et en devient le président ; il prend part au mouvement de désobéissance civile (baptisé « Comité des 100 ») et lance une action à Trafalgar Square en février 1961, suivie d'une marche sur Whitehall. D'autres réunions ont lieu à Hyde Park en août. Il est inculpé, arrêté, puis relâché. Il s'intéresse à tous les mouvements de libération : les combattants grecs de la Résistance (1963), les Palestiniens, etc. En novembre 1966, il constitue contre les crimes de guerre au Viêt Nam un tribunal international dont il fixe les objectifs en ces termes : « Puisse ce tribunal éviter le crime de silence. » Le tribunal se réunit en mai 1967 et est présidé par J.-P. Sartre ; Russell ne peut y assister à cause de son âge ; il meurt trois ans plus tard.

Parmi les œuvres de Russell, il faut encore citer : Mysticism and Logic and Other Philosophical Essays (1918), The Pratice and Theory of Bolchevism (1920), The Problems of China (1922), On Education (1926), The Analysis of Matter (1927), An Outline of Philosophy (1927), Marriage and Morals (1929), The Conquest of Happiness (1930), Education and the Social Order (1932), Power : a New Social Analysis (1938), Human Society in Ethics and Politics (1954).

La logique et la philosophie de Russell

Les fonctions propositionnelles

La logique à laquelle Russell croit possible de réduire les mathématiques (logicisme) comprend le calcul des propositions et le calcul des prédicats avec variables de prédicat quantifiées. Le nom de fonction propositionnelle, dont il emprunte à G. Frege l'idée, recouvre plusieurs conceptions.

a) La fonction propositionnelle comme énoncé ouvert

Un exemple en est « x est mortel », issu de la proposition « Socrate est mortel » quand on remplace le nom propre « Socrate » par une variable d'individu. En tant qu'énoncé ouvert, une fonction propositionnelle désigne une valeur de vérité ambiguë (elle n'est ni vraie ni fausse). Elle ne devient le nom d'une valeur de vérité qu'une fois que la ou les variables libres qui y figurent sont remplacées par des noms d'objets déterminés. « x est mortel » est vrai de Socrate, faux d'un objet éternel, par exemple pour « 2 » substitué à x.

b) La fonction propositionnelle comme prédicat avec variables en forme nominale

Ainsi, l'écriture ϕ xyz, six, y et z ne sont pas considérés comme des variables libres, mais comme des marqueurs de place destinés à montrer de combien d'arguments dépend ϕ, est un prédicat dans ce sens. L'équivoque des variables libres est que celles-ci peuvent jouer plusieurs rôles différents.

c) La fonction propositionnelle comme fonction logique

C'est-à-dire comme application d'un domaine d'individus (ou d'un domaine de n-uples d'individus) dans l'ensemble des valeurs de vérité : il s'agit alors non plus, comme dans a et b ci-dessus, d'un objet linguistique, mais d'un objet abstrait susceptible d'interpréter une fonction propositionnelle comme entité linguistique.

d) La fonction propositionnelle en tant qu'abstract ou en tant qu'attribut (ou nom d'attribut)

Lorsqu'on assigne des fonctions logiques aux fonctions propositionnelles, on adopte un principe d'extensionnalité : des fonctions logiques sont équivalentes exactement si elles sont vraies des mêmes objets. (En extension, une fonction logique est une classe.) Ce principe ne peut s'appliquer aux attributs sans les réduire aux classes. Russell semble hésiter à donner aux abstracts, c'est-à-dire aux expressions telles que 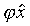, , 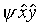etc., le statut (de noms) d'attributs ou celui (de noms) de classes. 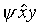peut se lire : le fait d'entretenir avec y la relation ψ.

L'implication formelle

La notion de fonction propositionnelle combinée à celle d'implication (⊃) permet de définir l'implication formelle. ϕ et ψ étant des fonctions propositionnelles à une place, ϕx ⊃ _xψx est une implication formelle, caractérisée par la récurrence, dans l'antécédent et dans le conséquent, de la même lettre liée par un quanteur portant sur toute l'expression.

Russell ne se borne pas à considérer les fonctions propositionnelles qui résultent d'une proposition par substitution de variables aux noms propres ou aux constantes, qui sont des valeurs particulières de leurs arguments (par exemple, de la substitution de x à a dans ϕa). Il considère aussi les fonctions propositionnelles qui résultent de ce qu'on fait varier ϕ : ainsi, on passe de ϕ(Socrate) à ψ(Socrate) ou à ∃ϕϕ(Socrate). Cette possibilité avait déjà été étudiée par Frege.

Les classes

Russell a eu plusieurs conceptions des classes. L'une d'elles est la théorie zigzag (1903 et 1906) : seules déterminent une classe les fonctions propositionnelles suffisamment simples. L'étude des paradoxes qui rendaient suspecte la notion de classe conduisit Russell à préférer une théorie « pas de classes », qui consiste à soutenir qu'on peut se servir de symboles de classe sans avoir pour autant à reconnaître l'existence des classes : la notion de classe représente une simple manière de parler, et les symboles de classe sont des abréviations. Il faut alors donner des règles permettant de traduire les expressions qui contiennent de tels symboles en d'autres expressions qui n'en contiennent plus. C'est une entreprise de réduction nominaliste. Techniquement, la réduction s'effectue au moyen de définitions contextuelles. Les classes s'introduisent sans qu'on ait besoin d'une notion nouvelle, « les x tels que ϕx » s'écrivant « {x : ϕx} », et « y ∊ {x : ϕx} » équivaut à « ϕy ». Sur la base de cette définition contextuelle, on peut développer l'algèbre booléenne des classes et (à partir d'une définition analogue) celle des relations. L'existence de ces objets est simulée (Quine), puisque ϕy peut partout remplacer y ∊ {x : ϕx} (chaque fois qu'on parle de la classe, on parle, en fait, des valeurs de vérité d'une fonction propositionnelle). Mais ce procédé devient inutilisable quand interviennent des classes de classes, qui sont nécessaires en théorie des nombres cardinaux. L'expression

{x : ϕx} ∊ α ≡ ∃ β [∀y(y ∊ β≡ ϕy) & β ∊ α],

qui permet d'éliminer l'abstract de classe {x : ϕx}, contient, en effet, des variables de classes liées.

La théorie des types

Les types peuvent être considérés comme des collections d'objets susceptibles d'être membres d'un même objet. Le type le plus bas sera constitué par les individus ; ensuite vient le type des classes dont les éléments sont des individus ; puis vient le type des classes de classes ; et ainsi de suite. Pour les relations binaires entre individus (classes de paires ordonnées), on aurait des types à deux dimensions, etc.

Par rapport au symbolisme logique, les types sont des domaines d'entités où les variables des différentes espèces (variables d'individu, de fonction propositionnelle d'individus, etc.) prennent leurs valeurs. Ce sont les « range of significance » des fonctions propositionnelles, c'est-à-dire les ensembles d'objets pour lesquels les valeurs de ces fonctions propositionnelles sont définies (autrement dit, les valeurs pour lesquelles ces fonctions sont vraies ou fausses). De plus, si x et y sont des expressions désignant des objets du même type, la substitution de y à x dans n'importe quel contexte changera éventuellement la valeur de vérité de ce contexte ; elle ne transformera pas une expression douée d'une valeur de vérité en une autre qui n'en a pas.

Par ailleurs, Russell traitait aussi les types comme des collections d'expressions ou comme des notations associées aux expressions. Une telle conception relève de la linguistique et non plus de l'ontologie. Ainsi, on parle parfois du type d'une expression ou d'attacher des indices de type aux expressions. Lorsqu'on a affaire au type d'une proposition (qui dépend du type des fonctions propositionnelles qui y figurent), le type est plutôt conçu comme une notation que comme un objet. Russell remarquait lui-même que la théorie des types est en fait une théorie des symboles plutôt que des entités (et, en effet, son propos est de définir les expressions bien formées).

Cette théorie des types fut suggérée à Russell par l'étude du paradoxe très élémentaire qui porte son nom, à savoir celui de la classe de toutes les classes qui ne sont pas éléments d'elles-mêmes. Pour empêcher la contradiction, Russell pose que x ∊ x et x ∉ x sont mal formés. D'une façon générale, l'expression figurant à gauche de ∊ doit être du type immédiatement inférieur à celui de l'expression qui apparaît à sa droite.

Étant donné la manière progressive dont se construisent les types, on n'a jamais C_α ∊ C_α pour un type α. Cette exclusion est la conséquence du principe du cercle vicieux (en abrégé PCV) sous la forme suivante : « Tout ce qui suppose la totalité d'une collection ne peut être un élément de cette collection » (en admettant qu'une collection se suppose elle-même) ; mais la théorie des types s'appuie sur des considérations de catégories sémantiques et de substitution qui préservent la correction grammaticale ; elle n'implique pas le PCV. Celui-ci a des conséquences plus fortes que l'exclusion des paradoxes triviaux. Une de ses versions dit qu'aucune totalité ne doit contenir comme éléments des objets qui ne sont définissables qu'en termes de cette totalité ou, plus précisément encore, « tout ce qui contient une variable apparente (=0 liée) ne doit pas être une valeur possible de cette variable » (1906, p. 634). Cela exclut ce qu'on appelle depuis lors, d'après Poincaré et Russell, les définitions imprédicatives. Ces définitions se caractérisent par le fait qu'un quanteur figurant dans le definiens parcourt un ensemble auquel appartient l'objet défini. On aura une définition de ce genre si l'on introduit un ensemble de nombres naturels par une expression renfermant un quanteur portant sur tous les ensembles de nombres naturels (tous inclut le nouvel ensemble qu'on est en train de définir).

Le PCV a pour conséquence qu'une collection d'ensembles ne doit pas être traitée comme achevée ; autrement dit, elle ne sera pas un domaine de valeurs pour une variable quantifiée.

On a appelé (Chwistek, Ramsey) théorie simple des types la hiérarchie des types indiquée ci-dessus et théorie ramifiée des types celle qui est conforme au PCV dans sa deuxième et sa troisième version : les définitions imprédicatives proscrites par le PCV ne sont pas en infraction avec la hiérarchie des types simples. La théorie ramifiée empêche aussi bien les paradoxes sémantiques ou épistémologiques que les paradoxes logiques.

Dans la théorie ramifiée, un ordre est attaché aux notations ou aux objets qui leur correspondent. Une fonction propositionnelle qui dépend d'une variable d'individu et qui devient une proposition par substitution à cette variable d'un nom d'individu est dite fonction du premier ordre (définition analogue pour le cas de plusieurs variables d'individu). Une fonction propositionnelle qui contient une variable de fonction 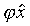liée par un quanteur ou par l'abstracteur sera dite fonction du second ordre. Par exemple, la fonction 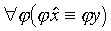, qui peut se lire « avoir toutes les propriétés de y », est d'ordre deux si ϕ est d'ordre un ; la fonction propositionnelle 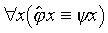, « être vrai d'exactement tous les objets qui vérifient ψ », dépend d'une variable ϕ liée par l'opérateur d'abstraction. Si ϕ est d'ordre un, 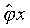est d'ordre deux, et l'expression totale est d'ordre deux ; si, en outre, ψ est d'ordre un, l'expression totale est une fonction prédicative, c'est-à-dire que son ordre est supérieur d'une unité à celui de son argument ψ ; sous forme non explicite, elle peut s'écrire ƒ !(ψ !x), le point d'exclamation indiquant la prédicativité (une fonction du premier ordre est automatiquement prédicative). Un autre exemple de fonction prédicative est la fonction propositionnelle 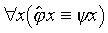déjà mentionnée, « avoir même extension que ψ », qui est prédicative lorsque 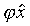et 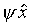sont d'ordre un, 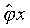étant alors d'ordre deux.

Au contraire, la fonction propositionnelle « avoir toutes les propriétés d'un grand général », qui se paraphraserait par

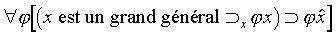
n'est pas du même ordre que « 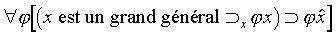 est un grand général », qui est une fonction d'individu, donc du premier ordre ; elle emporte une référence à toutes les fonctions propositionnelles 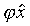du premier ordre ; elle est du second ordre et n'est pas prédicative.

La théorie ramifiée des types a pour conséquence qu'on n'a jamais plus à rencontrer ni à utiliser la notion d'ensemble quelconque. On n'aura affaire qu'à des ensembles définis par des conditions d'un certain ordre, et cela pour chaque type (les exemples qui précèdent n'ont mis en jeu que deux types : celui des individus et celui des classes d'individus ; bien entendu, le type des individus ne se ramifie pas). Une des conséquences particulières de la théorie ramifiée est que deux fonctions propositionnelles peuvent déterminer des classes identiques (c'est-à-dire les mêmes objets les vérifient, et tout objet qui est dans une de ces classes est aussi dans l'autre, et réciproquement), tout en étant d'ordre différent et donc distinctes. Cela montrerait que Russell est passé de la considération des classes et des relations à celle des attributs avec abandon de l'extensionnalité (ses fonctions propositionnelles sont implicitement devenues des [noms d'] attributs, point sur lequel a insisté Quine).

Cependant, le PCV étant très restrictif (il prohibe même les définitions inductives ; cf. Poincaré, « les Mathématiques et la logique », dans la Revue de métaphysique et de morale, n° 14, 1906, pp. 309-10) et la théorie ramifiée des types ayant pour effet de remplacer la notion de nombre réel par celle de nombre réel de différents ordres, Russell complète cette théorie par des axiomes de réductibilité qui affirment que pour toute fonction propositionnelle il en existe une qui lui est coextensive et qui est prédicative :

∀ψ ∃ϕ ∀x(ϕ !x ≡ ψx),

∀ψ ∃ϕ ∀x ∀y(ϕ !xy ≡ ψxy), etc.

L'affirmation selon laquelle des classes qui ne sont pas données par une fonction prédicative existent quand même constitue un axiome d'existence de classes ; Russell rétablit les imprédicativités interdites par le PCV ; il nullifie la construction progressive des fonctions propositionnelles des ordres supérieurs ; enfin, il fait disparaître les attributs au profit des classes et ramène l'extensionnalité.

Les historiens de la logique s'accordent à dire que « théorie ramifiée + axiome de réductibilité = théorie simple des types (dans un contexte extensionnel) ». Comme la théorie simple des types réussit à empêcher les paradoxes et comme la ramification paraît artificielle ou comporter des conséquences incommodes, on abandonna la théorie ramifiée.

Les descriptions

Russell avait commencé par réfléchir à l'analyse, proposée par Meinong, des termes sans dénotation, tels que « la montagne d'or ». Attendu qu'on ne peut pas classer la montagne d'or parmi les existants et qu'il y a pourtant une difficulté à dire que la montagne d'or n'existe pas (puisque cet énoncé mentionne quelque chose et qu'aucun énoncé ne peut porter sur rien), Meinong introduisait la notion de subsistants. Russell rejette cette théorie parce qu'elle reconnaît une sorte d'existence à des objets impossibles, ce qui est contradictoire.

Il n'adopte pas non plus la distinction proposée par Frege entre sens (« Sinn ») et dénotation (« Bedeutung »), qui aurait pu le conduire très simplement à ranger « la montagne d'or » parmi les expressions douées d'un sens et dépourvues de dénotation. Dans l'article de The Mind de 1905 et en d'autres occasions, l'emploi de « meaning » par Russell hésite entre sens et dénotation ou référence. Selon une mise au point de Geach, les couples de mots « meaning » et « dénotation », « Sinn » et « Bedeutung » ne se correspondent pas (du moins dans l'emploi que Russell fait des premiers), et le meaning russellien correspondrait plutôt à la Bedeutung de Frege. Par exemple, le meaning d'un terme singulier ou d'un nom propre est, d'après Russell, l'objet qui porte ce nom.

Russell pense échapper à la nécessité d'admettre des subsistants par sa théorie des descriptions. Une description permet de paraphraser les énoncés où figurent certains termes singuliers sans donner un équivalent direct de ces termes. Ainsi : l'actuel roi de France est chauve (1) se paraphrase d'abord en le x tel que x est l'actuel roi de France est chauve (2) et (2), où on vient de faire apparaître une description (« le x tel que … x … »), s'analyse en : il existe x tel que, quel que soit y [(y est un actuel roi de France exactement si y est identique à x) et x est chauve]. (3) L'énoncé (1) posait une énigme parce que son sujet grammatical ne désigne rien (en 1905) ; or, d'après (3), on voit que c'est un énoncé faux. (3) ne contient que des quanteurs, des variables, des fonctions propositionnelles et des fonctions de vérité. L'exemple montre que des énoncés où figurent des termes singuliers vides peuvent avoir un sens (une valeur de vérité) sans qu'on soit obligé de reconnaître l'existence d'objets qui n'existent pas. Dans (1), « l'actuel roi de France » est sujet apparent exactement comme « quelque chose » dans « quelque chose est blanc », et il disparaît du fait de sa paraphrase (3).

Le schéma général d'élimination est le suivant :

ψ(ιxϕx) ≡ ∃x[ϕx & ∀y(ϕy ≡ x = y)& ψx],

« le x tel que ϕx » étant symbolisé par ιxϕx. À la différence de Frege, Russell ne pose pas de convention pour la dénotation des descriptions impropres, c'est-à-dire pour le cas dans lequel ou bien aucun objet ne satisfait ϕ ou bien plus d'un objet satisfait ϕ. Dans de tels cas, Frege stipulait que ιxϕx désignerait une non-entité ou l'ensemble vide. Russell permet l'emploi d'une description même lorsque les prémisses de description ou formules d'unité associées à la fonction propositionnelle considérée ne sont ni prouvées ni admises comme hypothèses. Il en résulte, en particulier, que des formules comme ϕ(ιxϕx) ne sont pas vraies en général (si l'actuel roi de France n'existe pas ou s'il y en a plus d'un, la proposition « l'actuel roi de France est un actuel roi de France » est fausse) ; il en est de même de la loi d'extensionnalité suivante :

∀x(ϕx ≡ ψx) ⊃ ιxϕx = ι xψx,

qui n'est pas valide, son conséquent prenant la valeur « faux » lorsque ϕ et ψ sont identiquement fausses. L'exclusion des descriptions impropres cadre bien avec l'usage courant de la langue où celles-ci sont rares ; mais elle cadre moins bien avec la pratique des mathématiques, où des expressions telles que « la fonction qui tend vers l'infini le plus rapidement », etc., sont considérées comme parfaitement significatives et où il n'est pas rare d'introduire une description définie (ou la fonction qui en tient lieu) avant d'avoir prouvé l'existence et l'unicité. Leur exclusion semble toutefois nécessaire, eu égard à l'optique de Russell : à une description contradictoire (le carré rond par exemple) ne doit correspondre absolument aucun objet ; admettre une non-entité n'est pas conforme à la pensée de Russell.

D'autres logiciens (Strawson, On Referring, 1950) estiment que la théorie russellienne des descriptions, en assignant la valeur « faux » à toute phrase simple portant sur un inexistant, est infidèle à l'usage courant : « L'actuel roi de France est sage », qui présuppose la fausseté « L'actuel roi de France existe », n'est donc ni vrai ni faux. La critique de Strawson va surtout à l'encontre de tout essai d'enrégimentement du langage usuel dans le cadre d'analyse d'une logique symbolique.

En tout état de cause, le point capital de la théorie russellienne des descriptions est l'emploi d'un procédé renouvelé de J. Bentham (la paraphrase), et que Russell nomme procédé de la définition contextuelle, que par la suite il appliquera à l'élimination des symboles de classe, comme on l'a vu plus haut.

Philosophie des mathématiques et de la logique : le logicisme et son avenir

Sur le plan de l'ontologie, Russell s'est efforcé d'élucider le plus d'expressions possible comme étant des symboles incomplets. Telle est l'idée qui a présidé à sa paraphrase des descriptions et à sa réduction des classes aux fonctions propositionnelles.

En ce qui concerne les paradoxes, Russell a remarqué que l'infini actuel n'en est pas la cause. En théorie des ensembles, il a défini les nombres ordinaux comme des classes d'équivalence d'ensembles bien ordonnés modulo la relation d'isomorphisme ordinal ; il a défini les cardinaux comme des classes d'équivalence modulo la relation d'équinuméricité. À l'époque des Principia, il croyait facile de démontrer l'existence des ensembles infinis. Ensuite, il semble convaincu de la nécessité d'admettre que l'existence d'une infinité d'objets mathématiques relève d'un axiome.

Il s'en est toujours tenu à l'idée que la définition des entiers naturels dans la logique constituait le seul « fondement » valable de l'arithmétique. La doctrine logiciste des fondements, compte tenu des principes (choix, infini) inclus dans la logique des Principia et de la possibilité d'y quantifier sur les fonctions propositionnelles, se ramène à fonder les mathématiques sur la théorie des ensembles. Selon l'expression de Quine, la logique des Principia est en somme « de la théorie des ensembles déguisée ». Or, réduire les mathématiques à la théorie des ensembles est tout à fait possible, et Russell a lui-même, à la suite de Frege, contribué d'une manière décisive à le montrer. C'est un acquis définitif. Seulement, cette réduction n'est pas un fondement : c'est pour cela que le logicisme a disparu en tant que philosophie des mathématiques ; mais les apports techniques du logicisme (le développement du formalisme logico-mathématique) sont devenus le bien commun des logiciens.

Aujourd'hui il est facile de se livrer au petit jeu qui consiste à relever des imperfections ou des inadéquations dans ce qu'a pensé Russell : car, depuis lui, on a fait beaucoup mieux que lui. Vis-à-vis d'un créateur de l'envergure de Russell, la critique se doit de ne jamais tomber dans la mesquinerie.