suite géométrique
Suite de nombres réels (Un), n ∈ ℕ, telle qu'il existe un réel q (appelé raison) pour lequel, pour tout entier n, Un+1 = q Un.
MATHÉMATIQUES
Si q n'est pas nul et si U0= a, pour tout entier n, Un = aqn, relation qui permet l'étude de (Un).
Si q = 1, la suite est stationnaire ;
si q > 1 et U0 > 0, la suite est strictement croissante ;
si 0 < q < 1 et U0 > 0, la suite est strictement décroissante.
Dans ces deux derniers cas, les résultats sont inversés si U0 est négatif ;
si q < 0, la suite est alternée, les réels U2n ayant le signe de U0 et les réels U2n+1 le signe contraire.
La somme des n premiers termes d'une suite géométrique (Un),
Sn−1 = U0 + U1 + … + Un−1,
est égale à
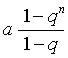 , si q ≠ 1, et à n. a, si q = 1.
, si q ≠ 1, et à n. a, si q = 1.



