coordonnées cartésiennes d'un point M
Coordonnées du vecteur
sur une base de l'espace vectoriel associé à En, O étant l'origine de l'espace affine.
GÉOMÉTRIE
Coordonnées cartésiennes
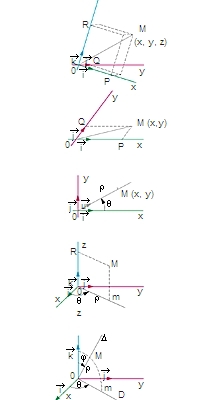
Dans l'espace muni d'un repère cartésien
[figure 1], tout point M est déterminé par
, où
, abscisse de M,
, ordonnée de M, et
, cote de M, sont les coordonnées cartésiennes du point M. En géométrie plane, on n'a besoin que de l'abscisse et de l'ordonnée (figure 2) ; sur la droite, que de l'abscisse.
Coordonnées polaires
Dans le plan muni d'un repère orthonormé direct
[figure 3], un point M est déterminé par la mesure θ de l'angle
[
, vecteur unitaire choisi sur la droite (OM)] et par le réel ρ tel que
. Le couple (ρ,θ) forme les coordonnées polaires de M. Coordonnées cartésiennes (x,y) et coordonnées polaires (ρ,θ) sont liées par x = ρ . cos θ et y =ρ . sin θ.
Coordonnées cylindriques
Dans l'espace affine E3 de dimension 3, on utilise parfois les coordonnées cylindriques (ρ,θ, z) où (ρ,θ) sont les coordonnées polaires de m, projection de M sur x Oy, et z est la cote de M (figure 4).
Coordonnées sphériques (figure 5)
Dans l'espace E3 rapporté au repère orthonormé
positif, les coordonnées sphériques de M sont (ρ,θ,ϕ) où :
,
et
.
Coordonnées cartésiennes (x,y,z) et coordonnées sphériques (ρ,θ,ϕ) sont liées par les relations
x = ρ . sin ϕ . cos θ, y = ρ . sin ϕ . sin θ
et z = ρ . cos ϕ.
