angle

Dénomination ancienne pour les notions actuelles de « secteur angulaire » ou de « mesure d'un secteur angulaire ».

GÉOMÉTRIE

Angle de couple de demi-droites

Deux couples (d, d′) et 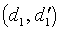sont en relation s'il existe une même isométrie directe f du plan, telle que f(d)=d′ et 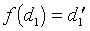. Cette isométrie unique est une rotation du plan. C'est une relation d'équivalence dont les classes d'équivalence sont les « angles de couple de demi-droites ». Celui de (d, d′) est noté 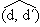. Chaque angle de couple de demi-droites est invariant dans une rotation plane, et il existe une bijection canonique de l'ensemble ℛ des rotations planes sur l'ensemble 𝓐 des angles de couple de demi-droites, sur lequel on peut transporter la structure de groupe commutatif de (ℛ, o).

Angle de paire de demi-droites

Deux paires {d, d′} et 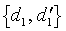sont en relation s'il existe une même isométrie f telle que f(d) = d′ et 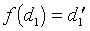. C'est une relation d'équivalence dont les classes d'équivalence sont les « angles de paire de demi-droites ». Celui de {d, d′} est noté 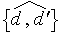. (On dit aussi angle géométrique.)