ℤ (suite)

• Étude de la relation d’ordre vis-à-vis de la multiplication.
Si 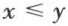, y – x ∈ ℤ⁺ et si z ∈ ℤ⁺, (y – x) z ∈ ℤ⁺ ou yz – xz ∈ ℤ⁺. D’où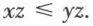
En revanche, si z ∈ ℤ^–,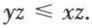
Ainsi, dans ℤ, une inégalité est conservée quand on multiplie ses deux membres par un nombre positif et renversée quand on les multiplie par un nombre négatif. ℤ, muni de +, × et 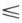est un anneau ordonné.

Pour tout élément x de ℤ, la valeur absolue de x est le plus grand des deux nombres x et – x ; on note | x | = sup (x, – x).
Si x ∈ ℤ⁺, | x | = x ; si x ∈ ℤ^–, | x | = – x.
Pour tous x et y de ℤ :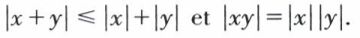

Divisibilité dans ℤ

Étant donné un nombre a de ℤ et un nombre b appartenant à l’ensemble ℕ* des entiers naturels non nuls, on peut classer le nombre a par rapport aux nombres de l’ensemble b ℤ = {x, x = bn, n ∈ ℤ}. Il se peut qu’il existe q ∈ ℤ tel que a = bq. Dans ce cas, on dit que b divise a. Si b ne divise pas a, on peut placer a entre deux nombres multiples consécutifs de b : bq < a < b (q + 1). Les deux cas peuvent être résumés :
— par la double inégalité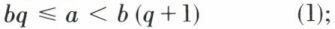
— par les relations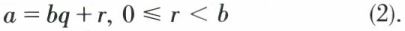

Les nombres q et r sont uniques. Les relations (2) caractérisent la division euclidienne, dans ℤ, de a par b. L’entier relatif q est le quotient à une unité près par défaut de a par b. L’entier naturel r est le reste de cette division.

Congruences arithmétiques

Étant donné un entier n ∈ ℤ, deux entiers x et x′ de ℤ ont même reste dans la division par n si, et seulement si, leur différence est un multiple de n. Dans ce cas, on dit que x et x′ sont congrus modulo n.

Dans ℤ, la relation x ℛ x′ ⇔ x – x′ = kn est une relation d’équivalence. On note x ≡ x′ (n). L’addition et la multiplication de ℤ sont compatibles avec la congruence modulo n
(x ≡ x′ et y ≡ y′) ⇒ x + x′ ≡ y + y′ et xx′ = yy′ (n).

Ainsi, on peut additionner ou multiplier membre à membre deux congruences modulo n.

L’ensemble-quotient 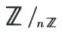de l’ensemble ℤ par la congruence modulo n, muni des opérations induites de celles de ℤ, l’addition et la multiplication, est un anneau commutatif et unitaire. Si n n’est pas un nombre premier,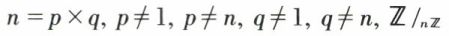

n’est pas intègre. En effet, 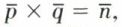la barre désignant la classe d’équivalence, mais 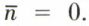D’où 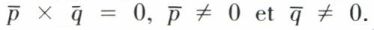Mais si n est premier, p et q n’existent pas et 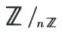est un corps.

Les congruences arithmétiques sont utilisées de façon courante en arithmétique et dans la théorie des nombres. Elles permettent de simplifier des calculs sur la divisibilité, puisque tout nombre est remplacé systématiquement par son reste, qui lui est inférieur ou égal. Elles sont un précieux instrument de démonstration.

Exemple. On veut savoir si le nombre 999 999 est divisible par 7.
999 999 = 10⁶ – 1 ; 10 ≡ 3 (7), d’où 10⁶ = 3⁶ (7).
Mais 3⁶ = (3²)³ = 9³ ≡ 2³ (7), puisque 9 ≡ 2 (7).
D’où 3⁶ ≡ 1 (7) et 10⁶ – 1 ≡ 3⁶ – 1 ≡ 1 – 1 ≡ 0 (7).

Le nombre 999 999 est divisible par 7.

E. S.

➙ Anneau / ℕ / ℚ / Relation binaire.

 A. Chatelet, Arithmétique et algèbre modernes (P. U. F., 1954-1956, 2 vol. ; nouv. éd., 1966, 3 vol.). / J. Itard, Arithmétique et Théorie des nombres (P. U. F., coll. « Que sais-je ? », 1963 ; 3^e éd., 1973) ; les Nombres premiers (P. U. F., coll. « Que sais-je ? », 1969). / C. S. Ogilvy et J. T. Anderson, Excursions in Number Theory (Fair Lawn, N. J., 1966 ; trad. fr. Excursions dans la théorie des nombres, Dunod, 1970). / O. Ore, Invitation to the Number Theory (Westminster, Maryland, 1969 ; trad. fr. Initiation à la théorie des nombres, Dunod, 1970).