norme dans un espace vectoriel sur ℝ (suite)
Propriétés d’une norme ou d’une semi-norme
• L’axiome (1) entraîne que f(0) = 0 puisque 0 = 0x, x ∈ E et, par suite, f(0) = f(0x) = 0f(x) = 0 ; mais la réciproque n’est pas nécessairement vraie. C’est pour cela que l’axiome (3) est nécessaire.
• Le même axiome entraîne que f est positivement homogène puisque 
et que f(λx) = λf(x) pour λ > 0 ; l’axiome (2) traduit la convexité de f.
• Toute combinaison linéaire positive, c’est-à-dire à coefficients dans ℝ+, de semi-normes est encore une semi-norme ; toute limite finie de semi-norme est aussi une semi-norme.
La norme (ou semi-norme) de x est notée || x ||.
Exemples de semi-normes
1. Un exemple trivial est fourni par le cas où E = ℝ et où l’on prend || x || = | x |, valeur absolue de x ; il est alors évident que les trois axiomes sont vérifiés et on a une norme.
2. Si E = ℝn, chaque vecteur de E a n composantes réelles, et à tout vecteur x de E on associe sup | ξi |, avec x = (ξ1, ξ2, ..., ξi, ..., ξn) ; || x || = sup | ξi |, i ∈ [1, n] est une norme sur E, car :
Enfin, | ξi | = 0 ne peut se produire que si tous les éléments ξi sont nuls, c’est-à-dire si x = 0. De même 
est une norme dans E = ℝn.
3. Si E = ℝn et si x = (x1, x2, ..., xn), l’application f : E → ℝ définie par
est une norme.
Les axiomes (1) et (3) sont évidents. Pour montrer l’axiome de convexité (2), il faut vérifier que 
ou pour i variant de 1 à n, que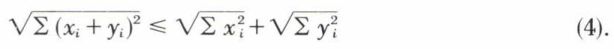
Cette inégalité est équivalente à
puis à
et enfin à
Pour démontrer l’inégalité (4′), on considère le trinôme en λ :
qui est positif ou nul ; son discriminant est
puisque le trinôme garde un signe constant ; l’inégalité (4′) en résulte.
4. Si φ(x) est une forme linéaire sur E, f(x) = | φ(x) | est une semi-norme sur E.
Distance associée à une norme
Si E est un espace vectoriel muni d’une norme f telle ∀ x ∈ E, 
l’espace E est dit « normé ». L’application d de E × E dans ℝ+, qui à tout couple (x, y) de vecteurs de E associe le nombre réel positif ou nul || x – y ||, satisfait aux conditions suivantes.
1. d(x, y) = d(y, x).
2. Pour tout triplet (x, y, z) de vecteurs de E,
3. Pour que deux vecteurs x et y soient égaux, il faut et il suffit que d(x, y) = 0.
4. Pour tout couple (x, y) de vecteurs de E et tout scalaire α ∈ ℝ, on a
d(αx, αy) = | α | d(x, y).
5. Pour tout triplet (x, y, z) de vecteurs de E, on a
d(x + z, y + z) = d(x, y).
Le nombre d(x, y) s’appelle distance des deux points x et y.
Ces propriétés sont des conséquences immédiates des axiomes définissant une norme dont elles ne sont souvent que des formulations différentes.
Espace métrique
Tout espace E sur ℝ, muni d’une norme, possède donc une distance d définie par
d(x, y) = || x – y ||, ∀x et y ∈ E.
Le couple (E, d) s’appelle un espace métrique. On peut alors considérer dans l’espace E une topologie associée à la métrique définie par la distance d.
1. Une boule ouverte ou fermée de centre a et de rayon ρ > 0 est l’ensemble B(a, ρ) des points x de E tels que 
(boule ouverte) ou (boule fermée). Si E = ℝ2, on remplace le mot boule par disque.
2. Une sphère de centre a et de rayon 
est l’ensemble S(a, ρ) des points de E tels que d(a, x) = ρ. Si E = ℝ2, on remplace le mot sphère par cercle.
3. Un ouvert de E est tout sous-ensemble A de E vide ou tel que ∀x ∈ A, il existe une boule ouverte de centre x et de rayon non nul contenue dans A.
On vérifie simplement que de tels ensembles satisfont aux trois axiomes qui définissent les ouverts d’un espace topologique :
• E et l’ensemble vide, Ø, sont ouverts ;
• toute réunion d’ouverts est un ouvert ;
• toute intersection finie d’ouverts est un ouvert.
La définition d’un ouvert indique que tout ouvert de E est une réunion de boules ouvertes. Inversement, toute réunion de boules ouvertes est un ouvert. Pour le démontrer, il suffit de montrer que toute boule ouverte est un ouvert puisque tout élément x appartenant à une réunion de boules ouvertes est contenu dans au moins une boule ouverte B(a ρ). Or la boule ouverte B [x, ρ – d(a, x)] est contenue dans B(a, ρ). En effet,
4. Des normes équivalentes sont des normes qui définissent la même topologie.
Dans l’espace vectoriel E sur ℝ, deux normes f1 et f2 définissent deux distances d1 et d2, d’où deux topologies. Pour que les deux topologies soient identiques, il faut et il suffit que toute boule B1 contienne une boule B2 et inversement. Pour qu’il en soit ainsi, il faut et il suffit qu’il existe deux constantes k et K positives telles que, ∀x ∈ E,
(on pourrait intervertir les indices).