ℝ

Symbole désignant l'ensemble des nombres réels ; symbole désignant la droite numérique achevée.

Une première définition des nombres réels est celle de nombres pouvant se mettre sous forme de développement décimal illimité. Une seconde, axiomatique, définit le corps ℝ des réels comme un ensemble muni d'une addition, d'une multiplication et d'une relation d'ordre notée ≤ possédant les propriétés suivantes :
– (ℝ, +, ×) est un corps commutatif ;
– (ℝ, +, ×, ≤) est un corps commutatif totalement ordonné ; la relation d'ordre total ≤ étant compatible avec l'addition et la multiplication dans ℝ ;
– toute partie non vide majorée de ℝ a une borne supérieure dans ℝ.

De ce troisième axiome, on déduit que ℝ est archimédien, dense dans lui-même (ℚ est aussi dense dans ℝ) et vérifie le théorème des segments emboîtés.

Les réels non rationnels sont appelés irrationnels. On distingue d'autre part les réels algébriques et les réels transcendants. Muni de la topologie associée à la distance 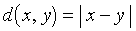, ℝ est appelé droite numérique et noté sous forme d'intervalle ]− ∞, + ∞[. Les intervalles ouverts bornés de ℝ sont les ouverts et les intervalles fermés bornés sont les fermés ; de plus, toute partie fermée bornée de ℝ est compacte, et tout ensemble infini borné possède au moins un point d'accumulation (théorème de Bolzano-Weierstrass). Dans la théorie des ensembles, l'ensemble des réels intervient dans la célèbre hypothèse du continu : tout ensemble non dénombrable contient une partie équipotente à ℝ ; il n'existe donc pas d'ensemble dont le cardinal soit strictement supérieur à Card (ℕ) et strictement inférieur à Card (ℝ).