triangulation
(bas latin triangulatio, mise en triangle)
Procédé géodésique ou topographique dans lequel on mesure les angles d'un ensemble de triangles.
GÉODÉSIE ET TOPOGRAPHIE
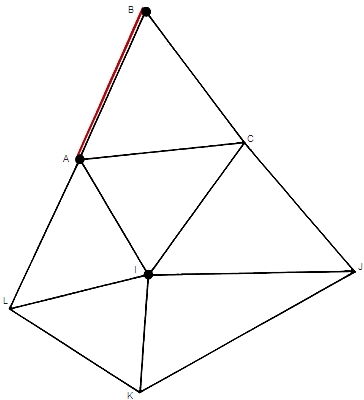
Inventée par Tycho Brahe à la fin du xvie s., appliquée par Snellius au début du xviie s., la triangulation repose sur le principe suivant : si, dans un triangle ABC, on connaît le côté AB et les angles
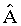et
, les côtés BC et AC se calculent de manière très simple par la relation des sinus :
.
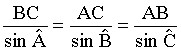
Les côtés BC et AC peuvent dès lors servir de côtés connus et ainsi de suite. Les points C, I, J, K, L, étant déterminés de proche en proche, peuvent servir de canevas d'ensemble. Le côté connu AB, mesuré directement, s'appelle la « base ». Pratiquement, le réseau de triangulation d'un grand pays comprend :
1° un point astronomique fondamental, qui sert d'origine des coordonnées géographiques et dont la position est déterminée par voie astronomique. Un azimut astronomique y fixe également la direction du côté de départ ;
2° un réseau de premier ordre, constitué par des triangles de forme régulière, dont les sommets sont distants de 30 à 40 km ; il comprend un cadre de chaînes méridiennes et parallèles enserrant dans leurs mailles le réseau de premier ordre complémentaire ;
3° un réseau de deuxième ordre (côtés de l'ordre de 15 à 20 km), s'appuyant sur le réseau primordial qui lui sert de cadre indéformable ;
4° un réseau de détail (3e et 4e ordre) de points distants de 5 à 6 km, sur lequel s'appuie le réseau de 5e ordre (densité : un point par kilomètre carré).
Les phases essentielles de l'élaboration d'une triangulation sont la reconnaissance, l'équipement, les observations et les calculs.
Les calculs de triangulation ont pour but de fixer les coordonnées géographiques (géodésiques) et rectangulaires des points observés. Les observations font l'objet d'un traitement d'ensemble (compensation), à l'issue duquel on obtient les positions géométriques précises du réseau triangulé.