rotation
(latin rotatio, de rotare, tourner)
Déplacement d'un espace affine euclidien
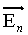ayant au moins un point invariant.
MATHÉMATIQUES
Dans le plan affine euclidien E2, une rotation (autre que la transformation identique) est caractérisée par la donnée du point invariant A, et de son angle α. La rotation r de centre A et d'angle α transforme un point M, différent de A, en M′ tel que : AM = AM′ et
.
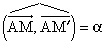Dans l'espace affine euclidien E2, les rotations (autres que la transformation identique) ont pour points invariants ceux d'une droite, appelée axe. Dans l'espace E2, orienté, si Δ est une droite, α un angle et d une des demi-droites de la direction de Δ, la rotation r d'un angle α autour de la droite orientée (Δ, d) transforme un point M, non situé sur Δ, en M′ tel que M et M′ ont la même projection orthogonale H sur Δ ; et HM = HM′ et α est un représentant du dièdre
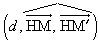. Le produit de deux rotations n'est une rotation que si les deux axes sont concourants ou s'ils sont parallèles, les deux angles étant alors non opposés.
L'ensemble des rotations vectorielles d'un espace vectoriel réel En de dimension finie non nulle n se note
; c'est un sous-groupe du groupe orthogonal
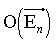de
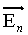(→ isométrie). Pour n = 1, il se réduit à l'identité. Pour n = 2, il est commutatif et isomorphe au groupe des angles de couple de demi-droites de
. Dans une base orthonormale directe de
, la matrice de la rotation d'angle α est de la forme
.
Dans le cas où n = 3, une rotation vectorielle autre que l'identité est une isométrie vectorielle dont le sous-espace vectoriel des vecteurs invariants est une droite vectorielle Δ. Une symétrie orthogonale par rapport à une droite est une rotation. Si
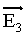est orienté, la rotation vectorielle d'angle α autour de D a pour matrice, dans une base orthonormale directe
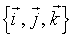telle que
soit le vecteur unitaire de D,
.
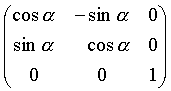
Deux rotations distinctes de l'identité ne commutent que si elles ont le même axe ou si ce sont deux symétries par rapport à des droites orthogonales.