oscillation

(bas latin oscillatio, -onis)

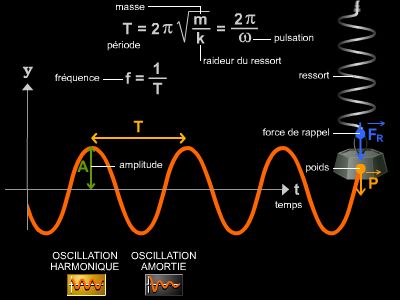
Phénomène caractérisé par une ou plusieurs grandeurs oscillantes.

Présentes dans presque tous les domaines de la physique, les oscillations font partie de notre univers quotidien. Cependant, la compréhension fine et rigoureuse des phénomènes périodiques n'a débuté qu'au xvii^e s. avec l'avènement des grands principes de la mécanique. La méthode développée s'est avérée très fructueuse, car, quelle que soit la nature du système, la description utilisée a une portée générale. Cet outil est aujourd'hui fondamental en acoustique, en électricité ou en construction technique.

Le mouvement périodique

Un phénomène est qualifié de « périodique » s'il se reproduit identiquement à des instants séparés par une durée constante, appelée période. Par exemple, les battements de cœur d'un individu au repos sont périodiques, avec une période de l'ordre d'une seconde.

L'inverse de la période s'appelle la fréquence. Son unité physique est le hertz (Hz). On donne parfois les fréquences en « périodes » car elles représentent le nombre d'oscillations par seconde. Ainsi, on appelle familièrement « le cinquante périodes » le courant alternatif du réseau, dont la fréquence est de 50 Hz.

L'approche la plus simple consiste en l'étude d'un système qui peut être décrit complètement par une seule variable. On parle alors de système à un seul degré de liberté.

L'oscillateur harmonique

On appelle oscillateur harmonique un mobile dont le mouvement est régi par une relation de proportionnalité entre son accélération et sa position par rapport à un point de référence. Le fait que la vitesse soit absente dans l'équation du mouvement a pour conséquence la conservation de l'énergie mécanique. Dans le modèle de l'oscillateur harmonique, on suppose que le mouvement n'est pas amorti. Cependant, quand l'amortissement est très faible, on peut l'utiliser et calculer le mouvement sur un intervalle de temps assez court, ce qui permet de négliger tout effet de dissipation. De plus, le terme de proportionnalité de la relation doit être négatif. L'équation mathématique du mouvement est donc : γ = Ax, où γ est l'accélération du mobile, x son déplacement, avec A < 0. En posant A = − ω² (ce qui est toujours possible, car A est négatif), on obtient l'équation de l'oscillateur harmonique : γ + ω² x = 0. Cette forme est intéressante, car elle permet de dire que le déplacement x du mobile, solution de cette équation, est une fonction sinusoïdale du temps, de pulsation ω.

Le système masse-ressort

L'oscillateur harmonique le plus simple et le plus facile à étudier est le système composé d'une masse et d'un ressort. Dans un premier temps, nous supposerons que ce système est installé sur un plan horizontal. Le ressort, dont la masse est négligeable, est fixé à l'une de ses extrémités en un point du plan ; on attache la masse à son autre extrémité. Pour que l'on puisse négliger l'amortissement du mouvement, il faut que le contact entre la masse et le plan se fasse avec le moins de frottements possible. On repère la position d'équilibre de la masse, puis on la déplace et on la lâche. Pour décrire le mouvement, on utilise le principe fondamental de la dynamique, lequel suppose l'égalité entre le produit de la masse par l'accélération et la somme de toutes les forces extérieures qui s'exercent sur le système. Quelles sont donc les forces qui agissent sur la masse ?

Il y a, bien sûr, l'action du ressort, mais aussi le poids et la réaction du plan sur la masse. Comme celui-ci est horizontal, ces deux dernières forces s'équilibrent ; il ne reste que l'action du ressort sur la masse. C'est une force de rappel, car elle tend à ramener la masse vers sa position d'équilibre, dont l'intensité est proportionnelle au déplacement par rapport à cette position. L'écriture mathématique du principe de la dynamique donne donc : mγ = − kx.

On a noté par m la valeur de la masse, par γ l'accélération du mobile, par k la raideur caractéristique du ressort, et par x le déplacement de la masse par rapport à sa position d'équilibre.

En divisant les deux termes par la masse, on exprime l'équation sous la forme classique des oscillateurs harmoniques :

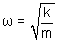
Le système est donc un oscillateur harmonique dont la pulsation est égale à la racine carrée du rapport de la raideur du ressort sur la masse :

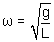
Le mouvement de la masse est sinusoïdal, de pulsation ω. Il est intéressant de constater que cette dernière est indépendante des conditions initiales du mouvement. Il en est évidemment de même de la période des oscillations, qui est proportionnelle à l'inverse de cette pulsation. Au lieu de faire osciller la masse sur un plan horizontal, on peut la suspendre au ressort et la faire osciller verticalement. On montre facilement que le système est encore un oscillateur harmonique, de même pulsation que précédemment.

Le pendule simple

Un pendule simple est formé d'une petite masse suspendue à un fil de longueur donnée. Si on l'écarte de sa position d'équilibre, il oscille en décrivant un arc de cercle. En examinant soigneusement les différentes forces qui s'exercent sur la masse puis en les reliant à l'accélération angulaire, on trouve que le pendule simple n'est pas un oscillateur harmonique pour toutes les amplitudes de mouvement. Cependant, le comportement du pendule se rapproche très fortement de celui d'un oscillateur harmonique pour de petites oscillations autour de la position verticale d'équilibre. Dans cette limite d'amplitude, le pendule simple est presque un oscillateur harmonique, dont la pulsation est égale à la racine carrée du rapport de l'accélération terrestre sur la longueur du fil :

La période d'oscillation dépend également des mêmes grandeurs physiques mais pas de l'amplitude initiale du mouvement, tant qu'elle reste petite. Galilée semble avoir été le premier à remarquer cet isochronisme des petites oscillations, en regardant, si l'on en croit la légende, un lustre se balancer pendant une messe interminable… C'est en tout cas cette propriété qui amène Christiaan Huygens, dès 1655, à utiliser le pendule pour réguler une horloge, dont la précision gagne ainsi, d'un seul coup, un facteur mille ; les modèles précédents, régulés par l'élasticité d'une lame, étaient moins précis encore que les horloges à eau. L'horloge à pendule parvient rapidement à tenir la seconde pendant vingt-quatre heures. Quant aux montres, elles vont aussi être régulées par un pendule, mais d'un tout autre type : un volant mobile autour d'un axe est rappelé vers sa position d'équilibre par un ressort spiral. Ce système est plutôt la transposition, dans un mouvement de rotation, du système masse-ressort traité plus haut. Le carré de sa pulsation est encore égal au rapport du terme de rappel sur le terme d'inertie. Le premier, toujours caractéristique du ressort, est un couple par angle de torsion, au lieu d'une force par mètre d'allongement. Le second, à la place de la masse, est le moment d'inertie du volant.

Le pendule près de l'équateur

En 1671, l'astronome français Jean Richer installe à Cayenne, en Guyane, un observatoire qui doit lui permettre d'effectuer, en collaboration avec Jean Dominique Cassini à Paris, la première mesure des dimensions du système solaire. Or Richer constate que le pendule d'une horloge bat plus lentement à Cayenne qu'à Paris. C'est donc que la pesanteur y est plus faible. Cette découverte permet à Isaac Newton, quelques années plus tard, de prédire l'aplatissement de la Terre aux pôles, ce qui implique, en effet, que Paris est plus près du centre de la Terre que Cayenne.

L'analogie électrique

Si l'on branche un condensateur chargé sur une bobine de résistance négligeable, on obtient un circuit où la charge électrique oscille entre les deux plaques du condensateur. L'égalité des tensions aux bornes de chacun des deux dipôles permet d'écrire une équation qui relie la charge q à sa dérivée seconde par rapport au temps :

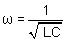
Le système est bien un oscillateur harmonique. Sa pulsation est l'inverse de la racine carrée du produit des caractéristiques des dipôles (L est l'auto-induction de la bobine, et C la capacité du condensateur) :

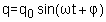
La charge électrique q, l'intensité i et la différence de potentiel U varient donc en fonction du temps de façon sinusoïdale :
q = q_oω sin(_ωt + φ)
i = q = q_oω cos(_ωt + φ)

Outre ses nombreuses applications en électronique, ce circuit permet de modéliser simplement un système masse-ressort ; la masse peut être représentée par l'auto-induction de la bobine, et la raideur du ressort par l'inverse de la capacité du condensateur. De la même façon, des circuits plus sophistiqués permettent de modéliser des systèmes de masses et de ressorts plus complexes, et donc de les étudier plus commodément ; il est en effet plus simple de tourner le bouton d'un condensateur variable que de modifier la raideur d'un ressort…

Par ailleurs, de même que le contact entre la masse et le plan était sans frottements, on remarque que la bobine est sans résistance. Dans les deux cas, il s'agit d'éviter l'amortissement.

L'amortissement

Si l'on ne néglige plus les frottements (ou la résistance globale, dans le cas du circuit), on introduit dans l'équation de la dynamique un terme supplémentaire, lié, le plus souvent, à la vitesse. Bien que les frottements puissent être dus à des causes très diverses, on ne s'intéresse ici qu'aux frottements visqueux, que l'on exprime dans l'équation du mouvement sous la forme d'une force dissipative, liée à la vitesse. On fait généralement l'hypothèse de proportionnalité entre cette force et la vitesse du mobile. Il existe, de façon analogue, un composant électrique, la résistance, qui provoque une chute de tension, proportionnelle à l'intensité de courant qui la traverse. Si la comparaison entre système mécanique et circuit électrique est encore possible, il n'y a cependant plus de comportement harmonique. La fonction décrivant le déplacement du mobile et celle décrivant la charge électrique ne sont plus sinusoïdales ; chacun des systèmes transforme en chaleur une partie de son énergie mécanique ou électrique, et les oscillations s'amortissent. Elles peuvent même disparaître si l'amortissement est suffisamment important. La limite de l'amortissement au-delà de laquelle il n'y a plus d'oscillations s'appelle l'amortissement critique. Dans le cas où il y a encore des oscillations, leur pseudo-période est plus grande que la période de l'oscillateur non amorti. Cette différence augmente avec l'amortissement.

Le temps de relaxation

Le temps de relaxation est une caractéristique de l'oscillateur amorti. Pour comprendre son rôle, on peut reprendre le système masse-ressort en ajoutant une force de frottement. Cette dernière, qu'on suppose proportionnelle à la vitesse, s'oppose toujours à l'avancement du système ; on justifie ainsi le signe négatif de cette force dans l'équation du mouvement. L'application du principe fondamental de la dynamique donne donc : m γ = – ; Av – kx, ou encore :

Comme on l'a vu pour l'oscillateur harmonique, le coefficient du déplacement correspond au carré de la pulsation de l'oscillateur non amorti. On le note ω²₀.

On définit le temps de relaxation du système par l'inverse du coefficient de la vitesse. En le notant par τ, l'équation du mouvement devient :

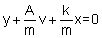
La pulsation de l'oscillateur non amorti ω₀ et le temps de relaxation τ décrivent complètement l'oscillateur amorti. Si l'amortissement est faible, la multiplication de ces deux caractéristiques donne une valeur très supérieure à l'unité. Ainsi, pour une corde de piano, qui doit être peu amortie pour émettre un son, ce produit est de l'ordre du millier. Un autre calcul montre que l'on atteint l'amortissement critique lorsque ce produit vaut 0,5.