mécanique statistique

Branche de la physique qui relie les propriétés des corps à l'échelle courante (ou macroscopique) à celles de leurs constituants microscopiques (atomes, molécules, etc.).

PHYSIQUE

Mécanique statistique

Les grandeurs physiques mesurables (pression, température, résistivité électrique, etc.) d'un système macroscopique ne peuvent être reliées aux propriétés de ses constituants microscopiques que par l'intermédiaire de concepts probabilistes. Le nombre de degrés de liberté d'un tel système est si grand (1 cm³ de gaz contient environ 10¹⁹ molécules…) qu'on ne peut le décrire exactement. En outre, la mesure, qui prend un certain temps, ne donne que des valeurs moyennes.

Plutôt que d'étudier le comportement d'un système au cours du temps, on peut examiner, à un instant donné, l'état d'un grand nombre de systèmes identiques et effectuer une moyenne sur cet ensemble. L'« hypothèse ergodique » postule que les deux modes de calcul donnent le même résultat : c'est le fondement de la mécanique statistique.

Entropie statistique, température, distribution de Boltzmann

Un état microscopique est déterminé par la donnée de l'état de chacun des éléments constituant le système. Si l'on connaît les probabilités P_e qu'a le système de se trouver dans chacun de ses états microscopiques e, il est possible de calculer les valeurs moyennes des grandeurs physiques macroscopiques par application des techniques statistiques. L'entropie, qui n'est pas seulement une valeur moyenne, est définie par : 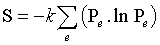, où k est la constante de Boltzmann. Mais tous les états microscopiques ne peuvent être atteints par le système. Des contraintes extérieures (le volume ou l'énergie doivent être constants) font que seuls certains états lui sont accessibles. L'hypothèse microcanonique postule que, pour un système isolé à l'équilibre, tous les états accessibles sont également probables. L'entropie statistique fait alors intervenir le nombre W d'états microscopiques accessibles et s'exprime selon la célèbre formule, gravée sur la tombe de L. Boltzmann : S = k ln W. La température thermodynamique T d'un système isolé est une grandeur essentiellement macroscopique qui ne peut être définie comme moyenne d'une quantité microscopique. Elle est définie à partir de l'entropie par : 1/T = ∂S/∂E, où ∂S/∂E est la dérivée de l'entropie par rapport à l'énergie. La température permet de définir la probabilité P_e pour qu'un système, en contact avec un thermostat de température invariable T, se trouve dans un état microscopique e d'énergie E_e : P_e = A exp (−E_e/k T), A étant une constante telle que la somme de toutes les probabilités soit égale à 1. Cette loi est appelée « distribution de Boltzmann ».

Systèmes de particules indiscernables : statistiques de Fermi-Dirac, Bose-Einstein, Maxwell-Boltzmann

Le fait qu'un système soit constitué de particules identiques change le décompte des états microscopiques accessibles et donc le calcul de l'entropie. Lorsque les particules sont des fermions, leur comportement est décrit par la statistique de Fermi-Dirac : le nombre moyen de particules qui se trouvent dans un état λ d'énergie ε_λ est : 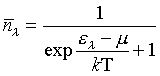, où μ est le niveau de Fermi déterminé par : 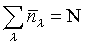, N étant le nombre total de fermions.

Lorsque les particules sont des bosons, leur comportement est décrit par la statistique de Bose-Einstein :

, où μ est une constante dépendant de la température et déterminée par 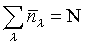, N étant le nombre total de bosons. À très basse température, cette statistique explique les phénomènes de superfluidité et de supraconductivité. À température élevée, les deux statistiques précédentes tendent vers celle de Maxwell-Boltzmann :

.