linéaire

MATHÉMATIQUES

Application linéaire

Si E et F sont deux espaces vectoriels sur un corps commutatif K, et f une application linéaire de E dans F, d'après la première propriété f(x + y) = f(x) + f(y), f est un homomorphisme de groupe de (E, +) dans (F, +) et a donc les mêmes propriétés que les homomorphismes, en particulier

f(0_E) = 0_F, f(−x) = −f(x).

Par application linéaire f, l'image d'un sous-espace vectoriel de E est un sous-espace vectoriel de F. Un cas particulier en est l'image f(E) de E, notée Im(f). La propriété « f est surjective » est alors équivalente à Im(f) = F.

Par application linéaire f, l'image réciproque d'un sous-espace vectoriel de F est un sous-espace vectoriel de E. Un cas particulier en est l'image réciproque du sous-espace formé par l'élément neutre 0_F de F, habituellement appelée noyau de f et notée Ker(f). La propriété « f est injective » est équivalente à Ker(f) = 0_E.

Si et sont respectivement des bases de E et F, f est entièrement déterminée par la connaissance des coordonnées sur (b_i) de chacun des n vecteurs f(a_i). En effet, si x est un élément de E, on a

et

∀i ∈ { 1, …, n}, f(a) élément de F s'exprime comme combinaison linéaire des vecteurs de la base (b_i). On appelle matrice de l'application linéaire f par rapport aux matrices (a_i) et (b_i) la matrice de type (p, n) dont la colonne d'indice i est formée des coordonnées de f(a_i) sur la base (b_i).

Équation linéaire

Si f est une application linéaire d'un K-espace vectoriel E dans un K-espace vectoriel F et b un élément de F, l'équation f(x) = b a des solutions si f⁻¹ (b) ;≠ . L'équation f(x) = 0, appelée équation linéaire homogène associée à f, admet pour solution les éléments de Ker f. Si x₀ est une solution de l'équation f(x) = b, on a f(x − x₀) = 0_F, et x = x₀ ∈ Ker f ; si x₀ est une solution de f(x) = b, les autres solutions sont donc de la forme x₀ + z, où z ∈ Ker f.

Système d'équations linéaires

Un système de p équations linéaires à n inconnues peut être mis sous la forme

.
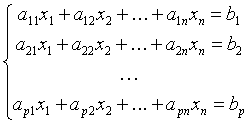
La matrice A [a_ij] est dite matrice des coefficients. Si l'on désigne par B la matrice colonne d'éléments b₁, b₂, …, b_p et par X la matrice colonne d'éléments x₁, x₂, …, x_n, le système équivaut à l'égalité matricielle AX = B.

Un système linéaire de n équations à n inconnues dont la matrice A a un déterminant non nul, admet une solution unique donnée par la relation matricielle X = A^{− 1}. B où A^{− 1} est la matrice inverse de A.