Équation de la forme P(x) = 0, où P(x) est un polynôme à coefficients dans K. [Si le degré de P(x) est n, alors P(x) = 0 est une équation algébrique de degré n.]

Pour l'équation du premier degré ax + b = 0,

si a ≠ 0, il y a une seule solution : x = − b/a ;

si a = 0 et b ≠ 0, pas de solution ;

si a = 0 et b = 0, une infinité de solutions.

Pour l'équation du second degré, ax² + bx + c = 0, les solutions dépendent de la quantité Δ = b² − 4ac, appelée discriminant ;

si Δ > 0, deux solutions réelles :

 ;

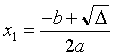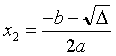 ; si Δ = 0, une solution double : x = − b/2a ; si

Δ < 0, deux solutions complexes conjuguées :

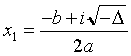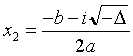 ; . Les coefficients du polynôme ax₂ + bx + c et les solutions sont liés par les relations x₁ + x₂ = − b/a ; x₁x₂ = c/a. En conséquence, si deux nombres ont pour somme S et pour produit P, ils sont solution de l'équation x² − S x + P = 0.