Barycentre d'un segment et d'un triangle
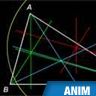
Barycentre d'un segment et d'un triangle
Si l'on considère un ensemble de points pondérés, c'est-à-dire affectés chacun d'un coefficient ou poids, on peut déterminer un point particulier G, appelé le barycentre de ces points (la somme des coefficients ne doit pas être nulle). Il est déterminé pour que la somme des vecteurs reliant tous les points à G, affectés du coefficient du point associé, soit nulle. Ce barycentre est le centre de gravité de l'ensemble des points. Il est simple de déterminer graphiquement le barycentre de deux points. Pour trouver le barycentre de trois points ou plus, on passe par des barycentres partiels.
© Larousse 2006