Johannes Kepler

Astronome allemand (Weil, aujourd'hui Weil der Stadt, Wurtemberg, 1571-Ratisbonne 1630).
Savant génial et obstiné, il est l'un des fondateurs de l'astronomie moderne. Sa découverte, purement empirique, des lois du mouvement des planètes a bouleversé la pensée de son époque et ouvert la voie à Newton.
Une enfance dure, mais une intelligence précoce
Johannes Kepler connaît une enfance assez dure, dans une ambiance familiale peu propice à l'éveil d'une vocation scientifique. Son père, mercenaire dans l'armée du duc de Wurtenberg, est un « soldat brutal, querelleur et immoral » souvent en campagne et qui finira par abandonner sa famille ; sa mère fera l'objet d'un procès en sorcellerie. Atteint de la variole à 3 ans, l'enfant en conservera toute sa vie des séquelles et une santé précaire. De 1574 à 1576, il vit chez ses grands-parents. Il accompagne ensuite ses parents à Leonberg, où il fréquente l'école latine. En 1584, il est admis au séminaire protestant d'Adelberg. Le duc de Wurtenberg le repère et décide de le prendre sous sa tutelle : en 1589, il rejoint l'université de Tübingen, où il reçoit une formation très complète. Son professeur d'astronomie, Michael Mästlin, lui enseigne le système de Copernic, dont il est un prudent défenseur. Diplômé de l'université en 1591, Kepler poursuit des études de théologie, avec le projet de devenir pasteur. Mais c'est finalement vers la science qu'il va se tourner, car il est nommé, en 1594, professeur de mathématiques à Graz. Lorsque, vers 1600, les persécutions religieuses contre les protestants l'obligent à quitter cette ville, il se réfugie à Prague, où il devient le disciple et l'assistant de l'astronome danois Tycho Brahe, auquel il succède, en 1601, comme astronome de l'empereur Rodolphe II.
Le découvreur des lois du mouvement des planètes
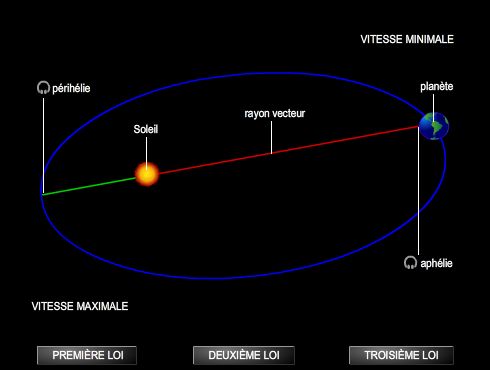
Devenu grâce à Mästlin un partisan convaincu de l'héliocentrisme, Kepler explique dans un premier ouvrage, le Prodomus… mysterium cosmographicum, publié en 1596, pourquoi le système de Ptolémée doit, selon lui, céder la place à la représentation copernicienne du monde. Mais, hanté par les idées pythagoriciennes, il croit l'Univers construit selon une architecture géométrique. Aussi élabore-t-il un ingénieux modèle géométrique du système de Copernic, dans lequel l'orbe de chaque planète occupe une sphère circonscrite à un polyèdre régulier et inscrite dans un autre. En fait, il a la conviction que le nombre de planètes, leurs distances au Soleil et leurs vitesses de révolution ne sont pas le fruit du hasard. Une étude systématique du mouvement de la planète Mars (dont la trajectoire reste mal interprétée par Ptolémée et par Copernic), après de laborieux calculs qu'il contrôle grâce aux observations précises de Tycho Brahe, le conduit à renoncer à l'hypothèse d'un mouvement circulaire – admise depuis Aristote – au profit d'une orbite elliptique. Ce travail amène Kepler à la découverte des deux premières lois qui vont immortaliser son nom. Il les publie en 1609 dans son Astronomia nova. La première énonce que chaque planète décrit dans le sens direct une ellipse dont le Soleil occupe un des foyers ; la seconde, que les aires décrites par le rayon vecteur allant du centre de la planète au centre du Soleil sont proportionnelles aux temps employés à les décrire. Kepler s'efforce ensuite de démontrer l'existence d'un rapport harmonique (au sens musical du terme) entre la plus grande et la plus petite vitesse des planètes. Il découvre ainsi la troisième loi fondamentale du mouvement des planètes, qu'il publie en 1619 dans son Harmonices mundi : les carrés des périodes de révolution des planètes sont proportionnels aux cubes des grands axes de leurs orbites.
Lors de leur publication, les lois de Kepler reçoivent un accueil mitigé : Galilée, par exemple, ne se ralliera jamais à l'idée du mouvement elliptique. Dans un premier temps, elles ne connaissent qu'un succès indirect : elles permettent de calculer des tables et des éphémérides astronomiques en excellent accord avec les observations. C'est Newton qui leur donnera une portée très générale, en montrant qu'elles découlent de la loi de l'attraction universelle et qu'elles s'appliquent à tout corps en mouvement orbital autour d'un autre, notamment aux satellites des planètes.
Dans les dernières années de sa vie, Kepler s'attache à établir des tables des positions des planètes, fondées sur les lois qu'il a mises en évidence. Cette tâche requiert de longs calculs, heureusement abrégés par l'invention récente des logarithmes. Elle aboutit à la publication, en 1627, des Tabulae rudolphinae (Tables rudolphines, ainsi nommées en hommage à l'empereur Rodolphe II), qui surpassent largement en précision toutes celles publiées auparavant.
Kepler meurt en 1630, dans un grand dénuement, mais livre encore, grâce à son gendre Jacob Bartsch (1600-1633), une œuvre posthume, Somnium seu astronomia lunari, véritable roman de science-fiction sur le thème du voyage vers la Lune.




