ℂ (suite)
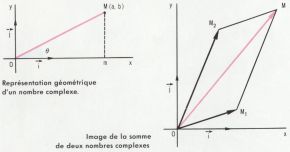
Somme de deux nombres complexes. La somme z = z1 + z2 des deux nombres complexes z1 et z2, d’images respectives M1 et M2, a pour image l’extrémité M du vecteur  somme géométrique des vecteurs
somme géométrique des vecteurs  et
et 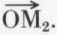 Ce résultat se généralise à la somme de plus de deux nombres complexes. On a l’inégalité
Ce résultat se généralise à la somme de plus de deux nombres complexes. On a l’inégalité
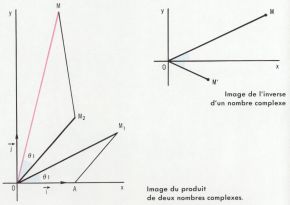
Produit de deux nombres complexes. Si
z1 = ρ1 (cos θ1 + i sin θ1) et z2 = ρ2 (cos θ2 + i sin θ2),
z = z1z2 = ρ1ρ2 [cos (θ1 + θ2) + i sin (θ1 + θ2)].
L’image M de z est telle que les deux triangles OAM1 et OM2M sont directement semblables. On généralise au produit de plusieurs nombres complexes. On a les deux relations
| z1z2 ... zn | = | z1 | | z2 | ....... | zn |
et
arg z1z2 ... zn = arg z1 + arg z2 + ... + arg zn.
Ainsi le module du produit de nombres complexes est égal au produit des modules des facteurs, et l’argument, à la somme des arguments.
Inverse d’un nombre complexe. Quotient de deux nombres complexes. L’inverse du nombre complexe z = ρ (cos θ + i sin θ) est le nombre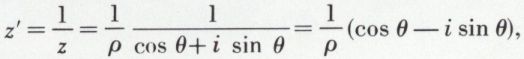
de module 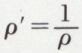 et d’argument θ′ = – θ(2π) ; on passe donc de l’image M de z à celle, M′, de z′ par le produit commutatif de l’inversion
et d’argument θ′ = – θ(2π) ; on passe donc de l’image M de z à celle, M′, de z′ par le produit commutatif de l’inversion 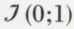 et de la symétrie d’axe Ox. Le quotient u de
et de la symétrie d’axe Ox. Le quotient u de
z1 = ρ1 (cos θ1 + i sin θ1) et z2 = ρ2 (cos θ2 + i sin θ2),
égal à 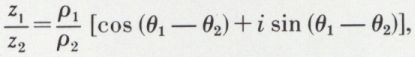 a pour module
a pour module 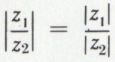 et pour argument
et pour argument 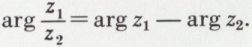
Racines n-ièmes d’un nombre complexe
Formule de Moivre. La puissance n-ième du nombre complexe z = cos θ + i sin θ a pour module 1n = 1 et pour argument nθ(2π) ; d’où la formule de Moivre :
(cos θ + i sin θ)n = cos n θ + i sin n θ.
Appliquée par exemple au cas n = 3, elle fournit les égalités
cos 3 θ = 4 cos3 θ – 3 cos θ et sin 3 θ = 3 sin θ – 4 sin3 θ.
La racine n-ième d’un nombre complexe z = ρ (cos θ + i sin θ) est un nombre complexe u = r (cos α + i sin α) tel que un = z, donc tel que
rn(cos n α + i sin n α) = ρ (cos θ + i sin θ),
d’où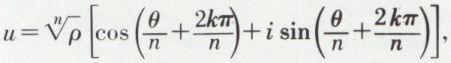
avec k = 0, 1, 2, ..., n – 1.
Les images des différentes solutions sont les sommets d’un polygone régulier de n côtés, inscrits dans un cercle de rayon 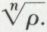 Si ρ = 1, r = 1 ; ces images sont sur le cercle trigonométrique de centre O et de rayon r = 1 : les racines n-ièmes de l’unité ont toutes pour module l’unité. Chacune d’elles étant donnée par
Si ρ = 1, r = 1 ; ces images sont sur le cercle trigonométrique de centre O et de rayon r = 1 : les racines n-ièmes de l’unité ont toutes pour module l’unité. Chacune d’elles étant donnée par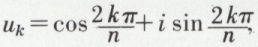
avec k = 0, 1, 2, ..., n – 1, ces racines forment un groupe multiplicatif cyclique d’ordre n
{u0, u1, ..., un–1}, avec un = u0.
Racine carrée d’un nombre complexe z. Si ce nombre est donné sous la forme z = ρ (cos θ + i sin θ), u2 = z si et seulement si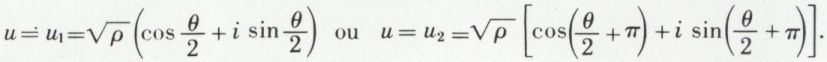
Les deux images sont symétriques par rapport à l’origine des axes ; les nombres u1 et u2 sont opposés, u2 = – u1.
Si le nombre complexe est donné sous la forme z = a + bi, u2 = (α + βi)2 = z si et seulement si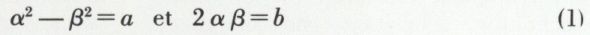
comme (α2 + β2)2 = (α2 – β2)2 + 4 α2 β2 = a2 + b2,
le système (1) est équivalent à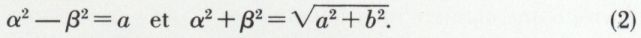
La résolution de (2) donne, par addition et soustraction,
Ces quantités sont positives quel que soit le signe de a ; d’où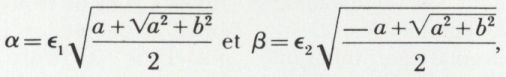
ε1 et ε2 étant égaux à + 1 ou à – 1, de façon que le produit de ε1 par ε2 soit égal au signe de b, puisque 2 α β = b. On trouve alors une solution, u1 = α1 + β1 i et une deuxième solution u2 = – u1 = – α1 – β1 i.
Le corps ℂ des complexes est le corps de décomposition du polynôme x2 + 1, puisque x2 + 1 = (x + i) . (x – i), et de tout polynôme à coefficients réels ou complexes ; un tel polynôme se décompose en effet dans ℂ en un produit de facteurs linéaires : on dit que ℂ est algébriquement clos.
Racines de l’unité
• Une racine primitive de l’unité est une racine qui engendre le groupe des racines n-ièmes de l’unité. La racine u1 est une racine primitive de l’unité, quel que soit n. Pour que la racine uk = u1k soit une racine primitive de l’unité, il faut et il suffit que k et n soient premiers entre eux. Ainsi, pour n = 8, il y a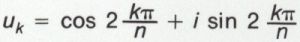
les quatre racines primitives u1, u3, u5, u7, qui engendrent le groupe des racines huitièmes de l’unité.
• Les racines cubiques de l’unité sont les nombres 1, j et j2, racines de l’équation z3 – 1 = 0.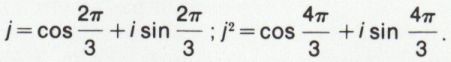
Les images de ces nombres sont les sommets d’un triangle équilatéral. Comme z3 – 1 = (z – 1) (z2 + z + 1), les nombres j et j2 sont liés par la relation 1 + j + j2 = 0, vérifiable sur la représentation géométrique. On a l’identité :
a3 + b3 + c3 – 3 abc = (a + b + c) (a + bj + cj2) (a + bj2 + cj),
a, b et c étant trois nombres réels ou complexes. Les puissances de j sont telles que j3p = 1, j3p+1 = j, j3p+2 = j2, p étant un entier positif, négatif ou nul.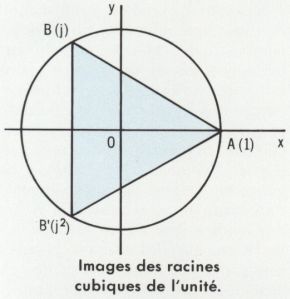
• Les racines quatrièmes de l’unité sont les nombres 1, i, i2 = – 1 et i3 = – i. Leurs images sont les sommets d’un carré. Les puissances du nombre i se répartissent ainsi :
i4p = 1 ; i4p+1 = i ; i4p+2 = – 1 ; i4p+3 = – i,
p étant un entier positif, négatif ou nul.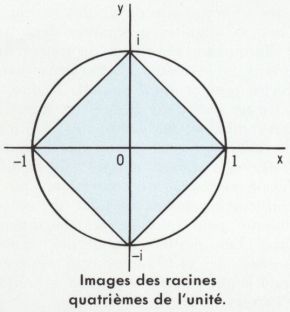
E. S.
➙ Algèbre / Algébrique / Anneau / Groupe / Opération.
J. Lelong-Ferrand et J.-M. Arnaudiès, Cours de mathématiques, t. I : Algèbre (Dunod, 1973). / E. Ramis, C. Deschamps et J. Odoux, Cours de mathématiques spéciales, t. I : Algèbre (Masson, 1974).




